Question

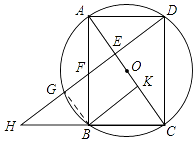
【题目】已知：如图，以矩形ABCD的对角线AC的中点O为圆心，OA长为半径作⊙O，过点B作BK⊥AC，垂足为K，过D作DH∥KB，DH分别与AC，AB，⊙O及CB的延长线相交于点E，F，G，H，且F是EG的中点．
（1）求证：点D在⊙O上；
（2）求证：F是AB的中点；
（3）若DE=4，求⊙O的半径和△BFH的面积．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，

∴AO=OC=OD=OB，

∵以O为圆心，OA长为半径作⊙O，

∴点D在⊙O上；

（2）证明：同理，点B也是⊙O上，

连接BG，

∵∠BAD=90°，

∴BD也是直径，

∴∠BGD=90°，

∵BK⊥AC，BK∥DH，

∴∠GEK=90°，

∴BG∥AC，

∴∠FAE=∠FBG，

∵F是EG的中点，

∴EF=FG，

∵∠AFE=∠BFG，

∴△AEF≌△BGF，

∴AF=BF，

∴F是AB的中点；

（3）证明：由（2）得：△AEF≌△BGF，

∴AE=BG，

∵OE⊥DG，

∴DE=EG=4，

∵OB=OD，

∴OE是△DGB的中位线，

∴OE= BG，

∴OE= AE，

设OE=x，则AE=2x，

∴OD=3x，

在Rt△OED中，由勾股定理得：OE2+ED2=OD2，

∴x2+42=（3x）2，

x= ，

∴OD=3 ，即⊙O的半径为3 ；

Rt△AED中，AE=2 ，ED=4，

∴AD= =2 ，

Rt△ABD中，BD=2OD=6 ，

AB= =4 ，

∵AF=BF，∠AFD=∠BFH，∠DAF=∠ABH=90°，

∴△AFD≌△BFH，

∴BH=AD=2 ，

BF=AF= AB=2 ，

∴S△BFH= BFBH= × =6 ．

【解析】（1）根据矩形的对角线相等且平分的性质得：OA=OD，所以点D在⊙O上；（2）证明△AEF≌△BGF，则AF=BF；（3）先在Rt△OED中，由勾股定理求⊙O的半径为3 ；再利用勾股定理计算AD= =2 ， AB= =4 ，证明△AFD≌△BFH，可得S△BFH= BFBH，代入计算即可．