
 如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$.
如图,⊙O的半径为6,AB是⊙O的直径,C、D是AB的三等分点,∠ECB=∠FDB=60°,则图中阴影部分的面积是6$\sqrt{11}$. 分析 连接OE,OF,延长EC交圆于G,连接OG、AG,作AM⊥EG于M,OH⊥EG于H,先证得△ACG≌△BDF,从而证得阴影部分的面积就是△AEG的面积,解特殊角的三角函数求得OH、AM,然后根据勾股定理和垂径定理求得EG,最后根据三角形的面积公式即可求得.
解答 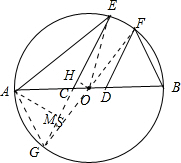 解:连接OE,OF,延长EC交圆于G,连接OG、AG,作AM⊥EG于M,OH⊥EG于H,
解:连接OE,OF,延长EC交圆于G,连接OG、AG,作AM⊥EG于M,OH⊥EG于H,
∵∠ECB=∠FDB=60°,
∴EG∥FD,
∴∠OCG=∠ODF,∠OGC=∠OFD,
在△COG和△DOF中,
$\left\{\begin{array}{l}{∠OCG=∠ODF}\\{∠OGC=∠OFD}\\{OC=OD}\end{array}\right.$,
∴△COG≌△DOF(AAS),
∴CG=DF,
在△ACG和△BDF中,
$\left\{\begin{array}{l}{AC=BD}\\{∠ACG=∠BDF=60°}\\{CG=BF}\end{array}\right.$,
∴△ACG≌△BDF(SAS),
∴阴影部分的面积就是△AEG的面积,
∵OC=2,∠ECB=60°,
∴OH=$\sqrt{3}$,
∴EH=$\sqrt{O{E}^{2}-O{H}^{2}}$=$\sqrt{33}$,
∴EG=2EH=2$\sqrt{33}$,
同理证得:AM=$\frac{\sqrt{3}}{2}$AC=2$\sqrt{3}$,
∴S△AEG=$\frac{1}{2}$EG•AM=$\frac{1}{2}$×2$\sqrt{33}$×2$\sqrt{3}$=6$\sqrt{11}$,
即阴影部分的面积为6$\sqrt{11}$.
故答案为6$\sqrt{11}$.
点评 本题考查了三角形旋转的性质,解特殊角的三角函数,勾股定理的应用,三角形面积公式等,证得△ACG≌△BDF是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
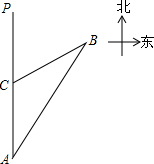 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点
如图,经过点A(0,-6)的抛物线y=$\frac{1}{2}$x2+bx+c与x轴相交于B(-2,0),C两点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com