

���� ��1���ٽ��ۣ�AB=CE����ͼ1�У���EH��BA��BP��H��ֻҪ֤����BDA�ա�HDE��EC=EH���ɽ�����⣻
�ڽ��ۣ�AB=$\sqrt{2}$CE����ͼ2�У���EH��BA��BP��H���ɡ�ABD�ס�EHD���ɵ�$\frac{AB}{EH}$=$\frac{AD}{DE}$=$\sqrt{2}$���Ƴ�AB=$\sqrt{2}$EH����֤��EC=EH�����ɽ�����⣻
��2�����ۣ�MN2=BM2+CN2������˵����BCC���ǵ���ֱ�������Σ�����C��BM�Ƶ�C��˳ʱ����ת90��õ���C��CG������GN��ֻҪ֤����C��MN�ա�C��GN���Ƴ�MN=GN����Rt��GCN�У�����GN2=CG2+CN2������֤����
��� �⣺��1���ٽ��ۣ�AB=CE��
���ɣ���ͼ1�У���EH��BA��BP��H��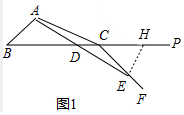
��AB��EH��
���B=��DHE��
��AD=DE����BDA=��EDH��
���BDA�ա�HDE��
��AB=EH��
�ߡ�PCF=��B=��CHE��
��EC=EH��
��AB=EH��
�ڽ��ۣ�AB=$\sqrt{2}$CE��
���ɣ���ͼ2�У���EH��BA��BP��H��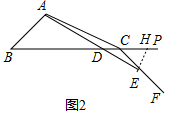
��BA��EH��
���ABD�ס�EHD��
��$\frac{AB}{EH}$=$\frac{AD}{DE}$=$\sqrt{2}$��
��AB=$\sqrt{2}$EH��
�ߡ�PCF=��B=��CHE��
��EC=EH��
��AB=$\sqrt{2}$EH��
��2�����ۣ�MN2=BM2+CN2��
���ɣ���ͼ3�У�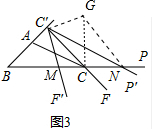
�ߡ�B=��PCF=��BCC��=45�㣬
���BCC���ǵ���ֱ�������Σ�
����C��BM�Ƶ�C��˳ʱ����ת90��õ���C��CG������GN��
�ߡ�C��CG=��B=45�㣬
���GCB=��C��CG+��C��CB=90�㣬
���GCN=90�㣬
�ߡ�MC��G=90�㣬��MC��N=45�㣬
���NC��M=��NC��G��
��C��M=C��G��C��N=C��N��
���C��MN�ա�C��GN��
��MN=GN��
��Rt��GCN����GN2=CG2+CN2��CG=BM��MN=GN��
��MN2=BM2+CN2��
���� ���⿼�鼸�α任�ۺ��⡢ƽ���ߵ����ʡ�ȫ�������ε��ж������ʡ����������ε��ж������ʡ�����ֱ�������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������λ����������ν�����⣬�����п�ѹ���⣮


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����1=��2����3=��4����5=��6����֤��ED��FB�����������Ͻ��ۻ����ݣ�
��ͼ����1=��2����3=��4����5=��6����֤��ED��FB�����������Ͻ��ۻ����ݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3x+$\frac{1}{2}$x=5-9 | B�� | -3x-$\frac{1}{2}$x=��-9��+��-5�� | C�� | $\frac{1}{2}$x+3x=��-9��+��-5�� | D�� | $\frac{1}{2}$x+3x=5+9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 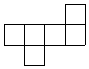 | B�� | 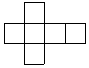 | C�� | 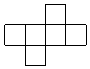 | D�� | 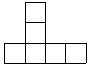 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com