
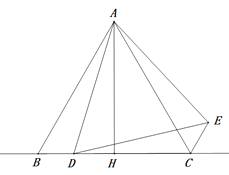
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:∠ABC=∠ACB;
(2)当D在线段BC上时,
①求证:△BAD≌△CAE;②当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)
【答案】(1)见解析;(2)①见解析;②D运动到BC中点(H点)时,AC⊥DE,理由见解析;(3)20°或40°或100°
【解析】
(1)证明Rt△AHB≌Rt△AHC(HL),即可解决问题.
(2)①根据SAS即可证明;②D运动到BC中点(H点)时,AC⊥DE;利用等腰三角形的三线合一即可证明;
(3)分三种情形分别求解即可解决问题;
解:(1)∵AB=AC,AH⊥BC,
∴∠AHB=∠AHC=90°,
在Rt△AHB和Rt△ACH中,
![]()
∴Rt△AHB≌Rt△AHC(HL),
∴∠ABC=∠ACB.
(2)①如图1中,
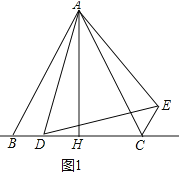
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
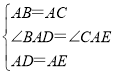
∴△BAD≌△CAE.
②D运动到BC中点(H点)时,AC⊥DE;
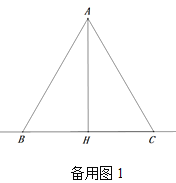
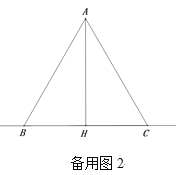
理由:如图2中,∵AB=AC,AH⊥BC,
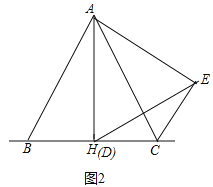
∴∠BAH=∠CAH,
∵∠BAH=∠CAE,
∴∠CAH=∠CAE,
∵AH=AE,
∴AC⊥DE.
(3)∠ADB的度数为20°或40°或100°.
理由:①如图3中,当点D在CB的延长线上时,
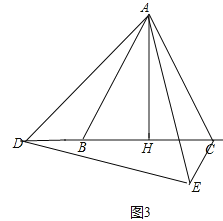
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC,
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,
∴△ABC是等边三角形,
∴∠ABC=60°
∵△ABD中的最小角是∠BAD=20°,则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ADB=180°-20°-60°=100°.
③当点D在BC 延长线上时,最小角只能是∠ADB=20°,
综上所述,满足条件的∠ABD的值为20°或40°或100°.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】雅美服装厂有A种布料70m,B种布料52米.现计划用这两种布料生产M、N两种型号的时装共80套,已知做一套M型号的时装共需A种布料0.6m,B种布料0.9m;做一套N型号的时装需要A种布料1.1m,B种布料0.4m.
(1)设生产x套M型号的时装,写出x应满足的不等式组;
(2)有哪几种符合题意的生产方案?请你帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象抛物线与
的图象抛物线与![]() 轴相交于不同的两点
轴相交于不同的两点![]() ,
,![]() ,且
,且![]() ,
,
(1)若抛物线的对称轴为![]() 求的
求的![]() 值;
值;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若该抛物线与![]() 轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴
轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴![]() 与
与![]() 轴相交点E,点F是直线
轴相交点E,点F是直线![]() 上的一点,点F的纵坐标为
上的一点,点F的纵坐标为![]() ,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.
,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1,2,3,4.小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球.
(1)请你用树状图或列表法列出所有可能的结果;
(2)求两次取得乒乓球的数字之积为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
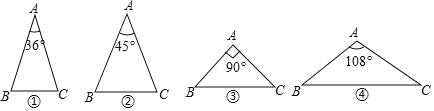
A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
①画线段AB;
②画射线CA、直线AD;
③过点B画AD的平行线BE;
④过点D画AC的垂线,垂足为F.

查看答案和解析>>
科目:初中数学 来源: 题型:
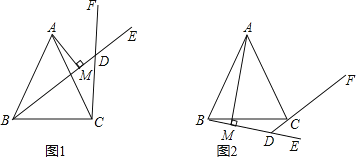
【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com