⊙O的半径r=5cm,圆心O到直线l的距离d=OD=3cm,在直线l上有三点P、Q、R,若PD=4cm,则P点在⊙O ;若QD=2cm,则Q点在⊙O ;若R点不在⊙O内,则满足的条件为: .
【答案】
分析:欲求点P、Q、R与圆O的位置关系,关键是求出线段OP、OQ的大小,再与半径r=5cm进行比较.若OP<r,则点P在圆内; 点OP=r,则点P在圆上;若OP>r,则点P在圆外.OQ也是同样的解法.若R点不在⊙O内,则OR>r,即RD>PD=4.
解答: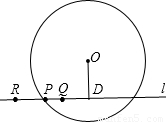
解:
⊙O的半径r=5cm,圆心O到直线l的距离d=OD=3cm,
则在Rt△POD中,OP=
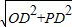
=
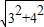
=5
∵OP=5=r
∴P点在⊙O上;
同理OQ=
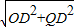
=
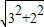
=
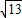
,Q点在⊙O内;
RD>4.
故答案为上,内,RD>4
点评:本题考查的是点与圆的位置关系,解决本题的关键是首先根据勾股定理算出点到圆心的距离,再比较点到圆心的距离与圆半径大小关系完成判定.

 解:
解: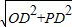 =
=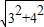 =5
=5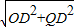 =
=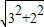 =
=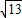 ,Q点在⊙O内;
,Q点在⊙O内;
