
����Ŀ����ͼ������y��ax2+ax+c��a��0����x��Ľ���ΪA��B��A��B����ߣ���AB��3����y�ύ��C���������߹���E����1��2����
��1���������ߵĽ���ʽ��
��2����x����·��Ƿ����һ��Pʹ�á�PBC�����Ϊ3�����������P������꣬������˵�����ɣ�
��3����DΪԭ�����A��ĶԳƵ㣬F������Ϊ��0��1.5��������CEF�Ƶ�C��ת������ת�����У��߶�DE��BF�Ƿ����ij�ֹ�ϵ��������λ�ã�����ָ����֤����Ľ��ۣ�
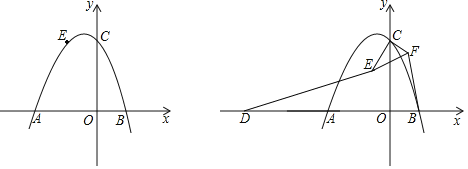
���𰸡���1��y����x2��x+2����2�����ڣ�P��3����10������3��DE��BF��DE��2BF��֤��������
��������
��1����������ó������ߵĶԳ���Ϊx��![]() ��
��![]() ������x��Ľ���ΪA��B��A��B����ߣ���AB��3�����A��B������꣬��A��E�������
������x��Ľ���ΪA��B��A��B����ߣ���AB��3�����A��B������꣬��A��E�������![]() �ɵ�a��c��ֵ���̶���������ߵĽ���ʽ��
�ɵ�a��c��ֵ���̶���������ߵĽ���ʽ��
��2����ΪS��ABC��3����PBC�������3��˵����Pһ���ڹ�Aƽ����BC��ֱ���ߣ���һ�����������ߵĽ��㣬��������A��ƽ����BC��ֱ�ߣ���������������һ����ô𰸣�
��3������DC��BC��֤����CDE�ס�CBF���������������ε����ʺ���ת�����ʼ��ɽ�����⣮
�⣺��1����Ϊ������![]() ��a��0���ĶԳ�����x��
��a��0���ĶԳ�����x��![]() ��
��![]() ��AB��3��
��AB��3��
����A��B�������������2��0������1��0����
����ΪE����1��2�����������ϣ�
�ѵ�A����2��0����E����1��2������![]()
![]()
���a����1��c��2��
����![]() ��
��
��2����ͼ��2����ʾ����A��BC��ƽ���߽��������ڵ�P��ƪ�����ޣ�P��δ����ʾ��ͼ�У���
��x��0����y��2
�ʵ�C�����ǣ�0��2��,
����ֱ��BC�Ľ���ʽΪ��y��kx+b��
B����������1��0����C����������0��2����
��![]() ��
��
��y����2x+2��
��A��BC��ƽ���߽��������ڵ�P��
��y����2x+b����A����2��0���������ʽ���ɵó���
���Թ�A���ֱ��Ϊy����2x��4��
���������Ľ�������Ϊ��
�ɩ�x2��x+2����2x��4��
���x1����2����ȥ����x2��3��
�����������ߵĽ���PΪ��3����10����
��3����ͼ��3����ʾ������DC��BC��
�������֪����D����4��0����F��0��1.5����
��DC��![]() ��
��![]() ��
��
BC��![]() ��
��
CE��![]() ��
��
CF��![]() ��
��
EF��![]()
��![]() ��
��![]()
�֡нǡ�DCE����BCF��
���CDE�ס�CBF������ECF��90����
��![]() ��CE��CF��
��CE��CF��
��DE��BF��DE��2BF��
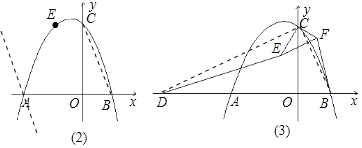


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����������ľ�����ȣ���
����������ľ�����ȣ���![]() ����������ľ���Ҳ��ȣ�
����������ľ���Ҳ��ȣ�
��1�����![]() ��
��![]() �����겢ֱ��д��
�����겢ֱ��д��![]() ����״��
����״��
��2������![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�����㣨�����
�ϵ�һ�����㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ����
����![]() Ϊ����������ʱ�����
Ϊ����������ʱ�����![]() �����ꣻ
�����ꣻ
��3������![]() Ϊ
Ϊ![]() ����һ���㣬��
����һ���㣬��![]() ����
����![]() Ϊб�ߵ�ֱ��������ʱ�����
Ϊб�ߵ�ֱ��������ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
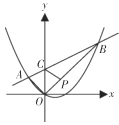
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() �����Բ������OA��OB��OC���ӳ�BO��AC���ڵ�D����
�����Բ������OA��OB��OC���ӳ�BO��AC���ڵ�D����![]() ���ڵ�F���ӳ�BA����G��ʹ��
���ڵ�F���ӳ�BA����G��ʹ��![]() ������FG.
������FG.
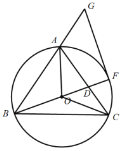
����ͼ
��1����֤��FG��![]() �����ߣ�
�����ߣ�
��2����![]() �İ뾶Ϊ4.
�İ뾶Ϊ4.
�ٵ�![]() ����AD�ij��ȣ�
����AD�ij��ȣ�
�ڵ�![]() ��ֱ��������ʱ����
��ֱ��������ʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У�A��BΪ���㣬A��2����3����B��4����3������ֱ��l��AB��P��l��һ���㣬l��AB�ľ���Ϊ6��M��N�ֱ�ΪPA��PB���е�����˵���У�
���߶�MN�ij�ʼ��Ϊ1���ڡ�PAB���ܳ��̶����䣻
�ۡ�PMN������̶����䣻 �������ڵ�Qʹ���ı���APBQ��ƽ���ı��Σ���Q��MN����ֱ�ߵľ����Ϊ9��
������ȷ��˵����_____��
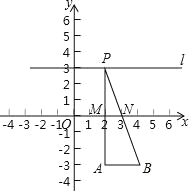
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC��һ�ŵ���ֱ�������β�ɫֽ��AC��BC����б���ϵĸ�CD��ȷ֣�Ȼ��ó�4�ſ�����ȵij�����ֽ����������4��ֽ���պÿ���Ϊһ��������������Ʒ��ߣ�ֽ�����ص�������ͼ2����������������Ʒ����ߺ����Ʒ�����֮��Ϊ_____��
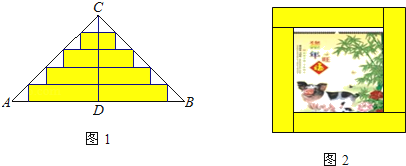
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����鳤��Ϊ�����꼶Ͷ��1��ԪΧһ�����ε��˶����أ���ͼ��������һ�߿�ǽ����������ѡ�ò�ͬ���Ͻ��������ߵ��ܳ�Ϊ![]() ��ǽ��
��ǽ��![]() ��ƽ����ǽ�ıߵķ���Ϊ200Ԫ/
��ƽ����ǽ�ıߵķ���Ϊ200Ԫ/![]() ����ֱ��ǽ�ıߵķ���150Ԫ/
����ֱ��ǽ�ıߵķ���150Ԫ/![]() ����ƽ����ǽ�ı߳�Ϊ
����ƽ����ǽ�ı߳�Ϊ![]() ��
��
��1�����˶��������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
��2�����˶����ص�������ʱ�Ƿ�ᳬ��Ԥ�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=![]() ��AD=3����E�ӵ�B��������BC���˶�����C������DE����E��DE�Ĵ��߽�AB�ڵ�F���ڵ�E���˶������У���EFΪ�ߣ���EF�Ϸ����ȱߡ�EFG�����EG���е�H��������·�����ǣ�������
��AD=3����E�ӵ�B��������BC���˶�����C������DE����E��DE�Ĵ��߽�AB�ڵ�F���ڵ�E���˶������У���EFΪ�ߣ���EF�Ϸ����ȱߡ�EFG�����EG���е�H��������·�����ǣ�������

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
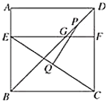
����Ŀ����ͼ��������![]() �ı߳�Ϊ12����
�ı߳�Ϊ12����![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() ������
������![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() ��
��![]() ��
��![]() ���㣮����
���㣮����![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬��
���е㣬��![]() �ij�Ϊ________��
�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
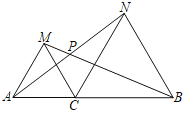
����Ŀ����ͼ����CΪ�߶�AB��һ�㣬��ACM���CBN���ǵȱ������Σ�AN��MB����P��
��1����֤��AN��BM��
��2������CP����֤��CPƽ�֡�APB��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com