
����Ŀ��С��Ͷ������һ�ֽ���Ϊÿ��20Ԫ�Ļ���̨�������۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ�����![]() �������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�80%��
�������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�80%��
��1����С��ÿ�»������Ϊw��Ԫ������ÿ�»������w��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ����ȷ���Ա���x��ȡֵ��Χ��
��2�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������ÿ�µ���������Ƕ��٣�
��3�����С����Ҫÿ�»�õ�����Ϊ2000Ԫ����ôС��ÿ�µijɱ���Ҫ����Ԫ�����ɱ������ۡ���������
���𰸡���1��w ![]() ��20��x��36����2�������۵��۶�Ϊ35Ԫʱ��ÿ�¿ɻ������������������2250Ԫ����3��4000Ԫ��
��20��x��36����2�������۵��۶�Ϊ35Ԫʱ��ÿ�¿ɻ������������������2250Ԫ����3��4000Ԫ��
��������
�����������1������ÿ�»������=һ����������ÿ��������y�����뻯�ɣ����������۹��������۵��۲����ڳɱ��ۣ���ÿ���������ڳɱ��۵�80%����ȷ���Ա���x��ȡֵ��Χ����2������1���еĺ�����ϵʽ�䷽��Ϊ����ʽ������������꼴�ɣ���3����W=2000�����x��ֵ�������Ա���x��ȡֵ��Χ������ȷ�����������x��ֵ��Ȼ����ÿ�µijɱ�ΪP��Ԫ����ȷ����P��x�Ĺ�ϵʽ����x��ֵ������㼴����
�����������1�������⣬�ã� w = ��x��20����y=��x��20������![]() ��
��![]() ��
��
��w ![]() ��20��x��36�� ��3+1����
��20��x��36�� ��3+1����
��2�����ں���w ![]() = ��10��x��35��2��2250
= ��10��x��35��2��2250
����x=35ʱ��W=2250
�𣺵����۵��۶�Ϊ35Ԫʱ��ÿ�¿ɻ������������������2250Ԫ����4����
��3��ȡW=2000�ã�![]()
��������̵ã�x1 = 30��x2 = 40��
��20��x��36
��ÿ�µijɱ�ΪP��Ԫ���������⣬�ã�
![]()
![]()
����x = 30ʱ��P��ֵ��С��P��Сֵ��4000��
����Ҫÿ�»�õ�����Ϊ2000Ԫ��С��ÿ�µijɱ�Ϊ4000Ԫ����4����


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����һ�ֲ�Ʒ2014��IJ�����100������ƻ�2016������ﵽ121���������2014�굽2016�����ֲ�Ʒ����������������ͬ��
��1����2014�굽2016�����ֲ�Ʒ�������������ʣ�
��2��2015�����ֲ�Ʒ�IJ���Ӧ�ﵽ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������9��x+1��2��4��x��1��2=0��ȷ�ⷨ�ǣ�������
A. ֱ�ӿ�����3��x+1��=2��x��1��
B. ��Ϊһ����ʽ13x2+5=0
C. �ֽ���ʽ��[3��x+1��+2��x��1��][3��x+1����2��x��1��]=0
D. ֱ�ӵ�x+1=0��x��l=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��x1��x2����x2012���Dz�����0��������������̽���������⣺
��1����y1=![]() ����
����![]() = ��
= ��
��2����y2=![]() ����
����![]() = ��
= ��
��3����y3=![]() ����
����![]() = ��
= ��
��4��������̽����֪��y2012=![]() ��
��![]() ���� ����ͬ��ֵ���������Щ��ͬ��y2012��ֵ�ľ���ֵ�ĺ͡�
���� ����ͬ��ֵ���������Щ��ͬ��y2012��ֵ�ľ���ֵ�ĺ͡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ����������ˮ��Դ��ij�в��ü۸���ص��ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѵ��շѱ����±���

���磺ij������1�·���ˮ8�����ף�Ӧ��ˮ��Ϊ2��6+4����8-6��=20��Ԫ����
������ϱ������ݽ���������⣺
��1����ij������2�·���ˮ5�����ף���Ӧ��ˮ�Ѷ���Ԫ��
��2����ij������3�·ݽ�ˮ��36Ԫ������ˮ��Ϊ���������ף�
��3����ij������4�·���ˮa������������6��a��10�������ú�a�Ĵ���ʽ��ʾӦ��ˮ����
��4����ij������5��6�����¹���ˮ18��������6�·���ˮ��������10������������5�·���ˮx�����ף����ú�x�Ĵ���ʽ��ʾ�û�����5��6�����¹���ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ʦ�����һ��̽���ܸ�ƽ��������ʵ�飺��һ������������ƽ����������߹̶�����A�з���һ��������ұ����B���������ƶ����з���һ�����������룬ʹ����������ƽ�⣮�ı�����B���O�ľ���x��cm�����۲�����B�����������y��g���ı仯�����ʵ�����ݼ�¼���±���
x��cm�� | 10 | 15 | 20 | 25 | 30 |
y��g�� | 30 | 20 | 15 | 12 | 10 |
��1���²�y��x֮��ĺ�����ϵ�����������ϵʽ��������֤��
��2�������������Ϊ24gʱ�������B���O�ľ����Ƕ��٣�
��3���������B�����ƶ�ʱ��Ӧ�������B�����ӻ��Ǽ������룿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱ���ABC��һ�㣬��AOB=110����BOC=![]() ,����BOC�Ƶ�C��˳ʱ�뷽����ת60����ADC������OD
,����BOC�Ƶ�C��˳ʱ�뷽����ת60����ADC������OD
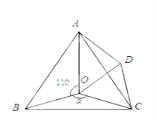
��1����COD��ʲô�����Σ�˵�����ɣ�
��2����AO=![]() ��AD=
��AD=![]() ,OD=
,OD=![]() ��
��![]() ����1������������
Ϊ����1������������![]() �Ķ���
�Ķ���
��3����![]() Ϊ���ٶ�ʱ����AOD�ǵ��������Σ�
Ϊ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() �ύ��A��1,0����
�ύ��A��1,0����![]() ����
����

��1����������ߵĽ���ʽ��
��2���裨1���е������߽�![]() ����
����![]() �㣬�ڸ������ߵĶԳ������Ƿ���ڵ�
�㣬�ڸ������ߵĶԳ������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ���ܳ���С�������ڣ����
���ܳ���С�������ڣ����![]() ������ꣻ�������ڣ���˵�����ɡ�
������ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�AB= 20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx����
�У�AB= 20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx����
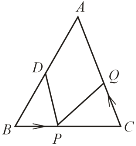
��1����AB=AC��P���߶�BC�ϣ���aΪ��ֵʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
��2����![]() ������������
������������![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3����![]() ����
����![]() �Ķ���Ϊ����ʱ��
�Ķ���Ϊ����ʱ��![]() Ϊ���������Σ�����ֱ��д���𰸣�����д����������
Ϊ���������Σ�����ֱ��д���𰸣�����д����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com