
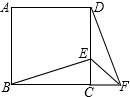
 如图所示,点E为正方形ABCD的边CD上的一点,F为边BC的延长线上一点,且CF=CE.若正方形ABCD的边长为2,且CE=x,△DEF的面积为y,请写出y与x之间的函数关系式为
如图所示,点E为正方形ABCD的边CD上的一点,F为边BC的延长线上一点,且CF=CE.若正方形ABCD的边长为2,且CE=x,△DEF的面积为y,请写出y与x之间的函数关系式为科目:初中数学 来源: 题型:
| 5 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
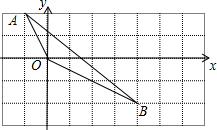 B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1.
B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1.查看答案和解析>>
科目:初中数学 来源: 题型:
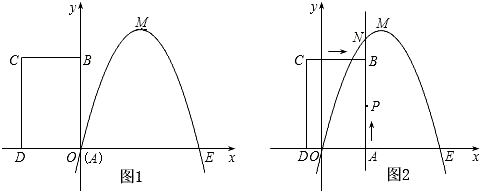
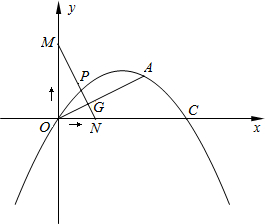 (2012•茂名)如图所示,抛物线y=ax2+
(2012•茂名)如图所示,抛物线y=ax2+| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:
(2013•遵义)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌(AB),放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB的高度(结果精确到0.1米,参考数据:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com