
【题目】历下区历史文化悠久,历下一名,取意于大舜帝耕作于历山之下。这位远古圣人为济南留下了影响深远的大舜文化,至今已绵延两千年.某校就同学们对“舜文化”的了解程度进行随机抽样调查,将调查结果绘制成如下两幅统计图:
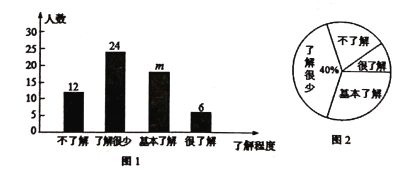
根据统计图的信息,解答下列问题:
(1)本次共调查 名学生,条形统计图中![]() ;
;
(2)若该校共有学生1200名,请估算该校约有多少名学生不了解“舜文化”;
(3)谓查结果中,该校九年级(2)班有四名同学相当优秀,了解程度为“很了解”,他们是三名男生、—名女生,现准备从这四名同学中随机抽取两人去市里参加“舜文化”知识竞赛,用树状或列表法,求恰好抽中一男生一女生的概率.
【答案】(1)60,18;(2)答:该校约有240名学生不了解“舜文化”;(3)![]() .
.
【解析】
(1)根据了解很少的有24人,占40%,即可求得总人数;利用调查的总人数减去其它各项的人数即可求得m的值;
(2)利用1200乘以不了解“舜文化”的人所占的比例即可求解;
(3)列出表格即可求出恰好抽中一男生一女生的概率.
本次调查的学生=24÷40%=60,
条形统计图中的m=60-12-24-6=18;
(2)![]() (人
(人![]() ,
,
答:该校约有240名学生不了解“舜文化”;
(3)列表如下:
男 | 男 | 男 | 女 | |
男 | (男,男) | (男,男) | (男,女) | |
男 | (男,男) | (男,男) | (男,女) | |
男 | (男,男) | (男,男) | (男,女) | |
女 | (女,男) | (女,男) | (女,男) |
由上表可知,共12种可能,其中一男一女的可能性有6种,分别是(男,女)三种,(女,男)三种,
![]() .
.


科目:初中数学 来源: 题型:
【题目】 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
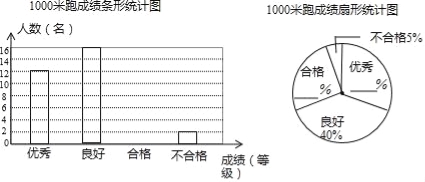
(1)根据给出的信息,补全两幅统计图;
(2)该校九年级有600名男生,请估计成绩未达到良好有多少名?
(3)某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
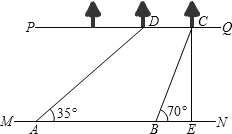
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接北京2022年冬奥会,某工艺厂准备生产奥运会标志与奥运会吉祥物,该厂主要用甲、乙两种原料.已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒,生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒.该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完.
(1)求该厂能生产奥运会标志和奥运会吉祥物各多少套?
(2)如果奥运会标志的成本为16元,奥运会吉祥物的成本为15元,若东营客商购进奥运会标志和奥运会吉祥物共250件进行试销,其中奥运会标志的件数不大于奥运会吉祥物的件数,且不小于80件,已知奥运会标志的售价为24元/件,奥运会吉祥物的售价为22元/件,且全部售出,设购进奥运会标志m件,求该客商销售这批商品的利润y与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,东营客商决定在试销活动中毎售出一件奥运会标志,就从一件奥运会标志的利润中捐献慈善资金a元,求该客商售完所有商品并捐献资金后获得的最大收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
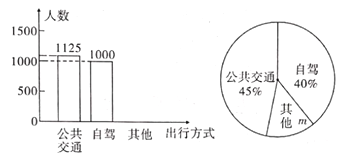
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
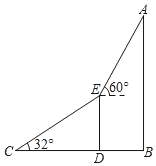
【题目】为庆祝改革开放40周年,深圳举办了灯光秀,某数学兴趣小组为测量“平安金融中心”AB的高度,他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后,测得“平安中心”AB的顶部A处的仰角为60°,(如图).已知C、D、B三点在同一水平直线上,且CD=400米,DB=200米.
(1)求大厦DE的高度;
(2)求平安金融中心AB的高度.
(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠ADB=90°,AB=2AD,BD的垂直平分线分别交AB,CD于点E,F,垂足为O.
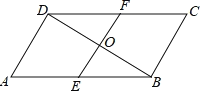
(1)求tan ∠ABD的值;
(2)求证:OE=OF;
(3)连接DE,BF,若AD=6,求DEBF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com