
【题目】如图1所示,已知函数y= (x>0)图像上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0) .动点M是y轴正半轴上点B上方的点.动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q.连接AQ,取AQ的中点C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时, 若四边形BQNC是菱形,面积为2,求此时P点的坐标.
(3)在(2)的条件下,在平面直角坐标系中是否存在点S,使得以点D、Q、N、S为顶点的四边形为平行四边
形,如果存在,请直接写出所有的点S的坐标;如果不存在,请说明理由.

【答案】(1)、3;(2)、(3,2);(3)、(1,4![]() ),(1,0),(5,4
),(1,0),(5,4![]() )
)
【解析】试题分析:(1)、连接OP,根据三角形的面积计算法则进行求解;(2)、根据四边形BQNC是菱形得出BQ=BC=NQ,∠BQC=∠NQC,根据AB⊥BQ,C是AQ的中点,得出BC=CQ=![]() AQ,∠BQC=60°,∠BAQ=30°,从而说明△ABQ和△ANQ全等,得出∠BAQ=∠NAQ=30°,∠BAO=30°,设CQ=BQ=x,根据菱形的面积求出x的值,即BQ的长度,根据Rt△AQB的勾股定理求出OA的长度,根据反比例函数的性质得出点P的坐标.
AQ,∠BQC=60°,∠BAQ=30°,从而说明△ABQ和△ANQ全等,得出∠BAQ=∠NAQ=30°,∠BAO=30°,设CQ=BQ=x,根据菱形的面积求出x的值,即BQ的长度,根据Rt△AQB的勾股定理求出OA的长度,根据反比例函数的性质得出点P的坐标.
试题解析:(1)、连接OP,S△PAB=S△PAO=![]() xy=
xy=![]() ×6=3
×6=3
(2)、∵四边形BQNC是菱形,∴BQ=BC=NQ,∠BQC=∠NQC
∵AB⊥BQ,C是AQ的中点,∴BC=CQ=![]() AQ,∴∠BQC=60°,∠BAQ=30°
AQ,∴∠BQC=60°,∠BAQ=30°
在△ABQ和△ANQ中 ∴△ABQ≌△ANQ ,∴∠BAQ=∠NAQ=30°,∴∠BAO=30°
∴△ABQ≌△ANQ ,∴∠BAQ=∠NAQ=30°,∴∠BAO=30°
∵S菱形BQNC=![]() =
=![]() ×CQ×BN,设CQ=BQ=x,则BN=2×(x×
×CQ×BN,设CQ=BQ=x,则BN=2×(x×![]() )=
)=![]() x,∴x=2,∴BQ=2
x,∴x=2,∴BQ=2
∵在Rt△AQB中,∠BAQ=30°,∴AB=![]() BQ=2
BQ=2![]() ,∵∠BAO=30°∴OA=
,∵∠BAO=30°∴OA=![]() AB=3,
AB=3,
又∵P点在函数y=![]() 的图象上,∴P点坐标为(3,2);
的图象上,∴P点坐标为(3,2);
(3)、![]() ·
·


科目:初中数学 来源: 题型:
【题目】某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):

(1) 写出该厂星期一生产工艺品的数量.
(2) 本周产量最多的一天比最少的一天多生产多少个工艺品?
(3) 请求出该工艺品厂在本周实际生产工艺品的数量.
(4) 已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年春节假期期间,我市接待旅游总人数达到9 186 000人次,比去年同期增长1.9%,将9 186 000用科学记数法表示应为( )
A. 9186×103 B. 9.186×105 C. 9.186×106 D. 9.186×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题中,其中正确的有( )
①圆的对称轴是直径;②等弦所对的弧相等;③圆心角相等所对的弦相等;④半径相等的两个半圆是等弧.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC和Rt△ADE中,AB=AC, AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读下列材料,并回答问题:
正常情况下,测得一弹簧的长度与悬挂物体的质量有下面一组对应值.
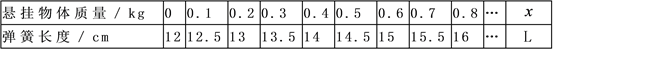
(1)直接用代数式表示正常情况下悬挂质量为![]() 的物体时弹簧的长度.
的物体时弹簧的长度.
(2)求悬挂质量为1.2kg的物体时弹簧的长度.
(3)若测得弹簧长度为20cm,判断此时所挂物体的质量是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(每小题5分,共10分)
(1)先化简,再求值5x2﹣[2xy﹣3(![]() xy+2)+4x2],其中x=﹣2,y=
xy+2)+4x2],其中x=﹣2,y= ![]() .
.
(2)若(2a﹣1)2+|2a+b|=0,且|c﹣1|=2,求c(a3﹣b)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com