
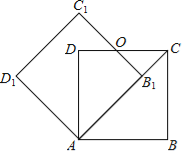
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.
连接AC1,

∵四边形AB1C1D1是正方形,
∴∠C1AB1=![]() ×90°=45°=∠AC1B1,
×90°=45°=∠AC1B1,
∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,
∴∠B1AB=45°,
∴∠DAB1=90°-45°=45°,
∴AC1过D点,即A、D、C1三点共线,
∵正方形ABCD的边长是1,
∴四边形AB1C1D1的边长是1,
在Rt△C1D1A中,由勾股定理得:AC1=![]() ,
,
则DC1=![]() -1,
-1,
∵∠AC1B1=45°,∠C1DO=90°,
∴∠C1OD=45°=∠DC1O,
∴DC1=OD=![]() -1,
-1,
∴S△ADO=![]() ×ODAD=
×ODAD=![]() ,
,
∴四边形AB1OD的面积是=2×![]() =
=![]() -1,
-1,
故选C.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=![]() 图象的两个交点.
图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
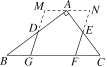
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,点D,E分别是AB,AC的中点,点G,F在BC边上(均不与端点重合),DG∥EF.将△BDG绕点D顺时针旋转180°,将△CEF绕点E逆时针旋转180°,拼成四边形MGFN,则四边形MGFN周长l的取值范围是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
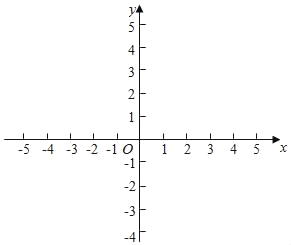
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线所对应的二次函数的表达式.
(2)直接写出该抛物线开口方向和顶点坐标.
(3)直接在所给坐标平面内画出这条抛物线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=12,AD平分∠BAC,交BC于点 E,交⊙O于点D,连接BD.
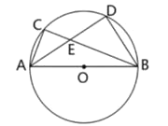
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
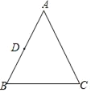
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列一元二次方程
(1) (2x-1)2=25
(2) 3x2-6x-1=0
(3) x2-4x-396=0
(4) (2-3x)+(3x-2)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有四个小球,上面分别标有数字-2,-1,0,1,它们除了数字不一样外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是__________.
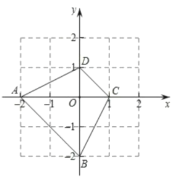
(2)小聪先从袋子中随机摸出一个小球,记下数字作为点![]() 的纵坐标,如图,已知四边形
的纵坐标,如图,已知四边形![]() 的四个顶点的坐标分别为
的四个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,请用画树状图或列表法,求点
,请用画树状图或列表法,求点![]() 落在四边形
落在四边形![]() 所围成的部分内(含边界)的概率.
所围成的部分内(含边界)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com