
分析 分两种情况:①当点E在线段AD上时,由四边形ABCD是平行四边形,可证得△EFD∽△CFB,求出DE:BC=2:3,即可求得EF:FC的值;
②当点E在射线DA上时,同①得:△EFD∽△CFB,求出DE:BC=4:3,即可求得EF:FC的值.
解答 解:∵AE=$\frac{1}{3}$AD,
∴分两种情况:
①当点E在线段AD上时,如图1所示
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△EFD∽△CFB,
∴EF:FC=DE:BC,
∵AE=$\frac{1}{3}$AD,
∴DE=2AE=$\frac{2}{3}$AD=$\frac{2}{3}$BC,
∴DE:BC=2:3,
∴EF:FC=2:3;
②当点E在线段DA的延长线上时,如图2所示:
同①得:△EFD∽△CFB,
∴EF:FC=DE:BC,
∵AE=$\frac{1}{3}$AD,
∴DE=4AE=$\frac{4}{3}$AD=$\frac{4}{3}$BC,
∴DE:BC=4:3,
∴EF:FC=4:3;
综上所述:EF:FC的值是$\frac{2}{3}$或$\frac{4}{3}$;
故答案为:$\frac{2}{3}$或$\frac{4}{3}$.
点评 此题考查了相似三角形的判定与性质与平行四边形的性质.此题难度不大,证明三角形相似是解决问题的关键;注意分情况讨论.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>3 | B. | m<3 | C. | m>-3 | D. | m<-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.8x-10=90 | B. | 0.08x-10=90 | C. | 90-0.8x=10 | D. | x-0.8x-10=90 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
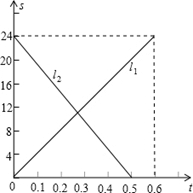 甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)的函数关系,则下列说法:
甲、乙两辆摩托车分别从A、B两地出发相向而行,图中l1、l2分别表示两辆摩托车与A地的距离s(千米)与行驶时间t(小时)的函数关系,则下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com