练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：

    x

    …

    -2

    -1

    0

    1

    2

    …

    y

    …

    11

    6

    3

    2

    3

    …

    则当y≤6时x的取值范围是______．

    【答案】-1≤x≤3

    【解析】

    由当x=0及x=2时y=3可得出二次函数图象的对称轴及顶点坐标，由其顶点纵坐标小于其他点的坐标可得出a＞0，由当x=-1时y=6可得出当x=3时y=6，再利用二次函数的性质即可得出当y≤6时x的取值范围．

    解：∵当x=0及x=2时，y=3，

    ∴二次函数图象的对称轴为直线，二次函数图象的顶点坐标为（1，2）．

    ∵y=2为最小值，

    ∴a＞0．

    ∵当x=-1时，y=6，

    ∴当x=3时，y=6．

    又∵a＞0，

    ∴当-1≤x≤3时，y≤6．

    故答案为：-1≤x≤3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠B=90°∠A

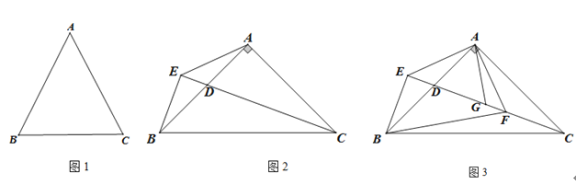
    (1)如图1，求证：AB=AC；

    (2)如图2，若∠BAC=90°，点D为AB上一点，过点B作直线CD的垂线，垂足为E，连接AE， 求∠AEC的度数；

    (3)如图3，在(2)的条件下，过点A作AE的垂线交CE于点F，连接BF，若∠ABF-∠EAB=15°，G为DF上一点，连接AG，若∠AGD=∠EBF，AG=6,求CF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC 是等边三角形，点 P 在△ABC 内，PA=2，将△PAB 绕点 A 逆时针旋转得到△P1AC，则 P1P 的长等于（ ）

    A. 2 B. C. D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某文化用品商店用元采购一批书包，上市后发现供不应求，很快销售完了.商店又去采购第二批同样款式的书包，进货单价比第一次高元，商店用了元，所购数量是第一次的倍.

    （1）求第一批采购的书包的单价是多少元？

    （2）若商店按售价为每个书包元，销售完这两批书包，总共获利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c的图象如图所示，对称轴为x=1，经过点（-1，0），有下列结论：①abc＜0；②a+c＞b；③3a+c=0；④a+b＞m（am+b）（其中m≠1）其中正确的结论有（　　）

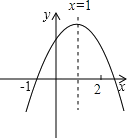
    A. 1个

    B. 2个

    C. 3个

    D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

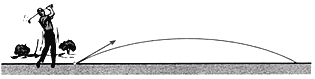
    【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度h（m）与它的飞行时间（s）满足二次函数关系，t与h的几组对应值如下表所示：

    t（s）

    0

    0.5

    1

    1.5

    2

    …

    h（m）

    0

    8.75

    15

    18.75

    20

    …

    （1）求h与t之间的函数关系式（不要求写t的取值范围）；

    （2）求小球飞行3s时的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于代数式ax2+bx+c(a≠0)，下列说法正确的是（ ）

    ①如果存在两个实数p≠q，使得ap2+bp+c=aq2+bq+c，则a+bx+c=a（x-p）（x-q）

    ②存在三个实数m≠n≠s，使得am2+bm+c=an2+bn+c=as2+bs+c

    ③如果ac＜0，则一定存在两个实数m＜n，使am2+bm+c＜0＜an2+bn+c

    ④如果ac＞0，则一定存在两个实数m＜n，使am2+bm+c＜0＜an2+bn+c

    A. ③ B. ①③ C. ②④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

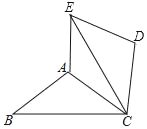
    【题目】如图，△ABC中，∠ACB中，∠ACB=30°，将△ABC绕点C顺时针旋转60°得到△DEC，连接AE．

    （1）求证：△ABC≌△AEC；

    （2）若AB=AC，试判断四边形ACDE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

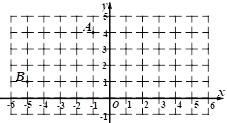
    【题目】点A（1,4）和点B（5,1）在平面直角坐标系中的位置如图所示:

    （1）点A1、B1分别为点A、B关于y轴的对称点，请画出四边形AA1B1B，并写出A1、B1的坐标;

    （2）在（1）的条件下，画一条过四边形AA1B1B的一个顶点的线段，将四边形AA1B1B分成两个图形，并且使分得的图形中的一个是轴对称图形.

    查看答案和解析>>

    同步练习册答案