练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列说法正确的是（　　）
    A．若ac=bc，则a=bB．若$\frac{a}{c}$=$\frac{b}{c}$，则a=bC．若$\frac{a}{2}$=$\frac{b}{4}$，则a=2bD．若a2=b2，则a=b

    分析 根据等式的性质，可得答案．

    解答 解：A、c=0时，两边都除以c，无意义，故A错误；
    B、两边都乘以c，故B正确；
    C、两边乘以不同的数，故C错误；
    D、a2=b2，则a=±b，故D错误；
    故选：B．

    点评 本题考查了等式的性质，熟记等式的性质是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．如图，在△ABC中，∠B=∠ACB，CD平分∠ACB，若∠ADC=78°，则∠A=76°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，平行四边形ABCD中，BE平分∠ABC交AD于E点，已知AB=5，AD=6，则DE长为（　　）
    A．1B．1.5C．2D．2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图所示，一棵大树高8米，一场大风过后，大树在离地面3米处折断倒下，树的顶端落在地上，则此时树的顶端离树的底部有（　　）米．
    A．4B．6.5C．5D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．在直线l上截取线段AB，使AB=6cm，再截取BC，使BC=3cm，则线段AC的长为（　　）
    A．9cmB．3cmC．3cm或9cmD．6cm或9cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

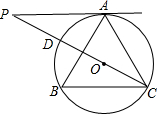    8．如图，在△ABC中，∠B=60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点P，CP交⊙O于点D，若AC=3，则△APC的面积为（　　）
    A．3$\sqrt{3}$B．$\frac{3}{2}$C．$\frac{3}{2}$$\sqrt{3}$D．$\frac{9}{4}$$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．小华在解题时发现二元一次方程□x-y=4中，x的系数已经模糊不清（用“□”表示），但查看答案$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$是这个方程的一个解，则□表示的数为$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．对于任意一个多位数，如果他的各位数字之和除以一个正整数n所得的余数与他自身除以这个正整数n所得余数相同，我们就称这个多位数是n的“同余数”，例如：对于多位数1345，1345÷3=448…1，且（1+3+4+5）÷3=4…1，则1345是3的“同余数”．
    （1）判断四位数2476是否是7的“同余数”，并说明理由．
    （2）小明同学在研究“同余数”时发现，对于任意一个四位数如果是5的“同余数”，则一定满足千位、百位、十位这三位上数字之和是5的倍数．若有一个四位数，其千位上的数字是十位的上数字的两倍，百位上的数字比十位上的数字大1，并且该四位数是5的“同余数”，且余数是3，求这个四位数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知在同一平面内∠AOB=90°，∠AOC=60°．
    （1）画∠AOC（不写画法，保留画图痕迹），则∠COB的度数为30°或150°；
    （2）画OD平分∠BOC，OE平分∠AOC，则∠DOE的度数为45°；
    （3）在（2）的条件下，将题目中的∠AOC=60°改成∠AOC=2a（a＜45°）其它条件不变，你能求出∠DOE的度数吗？若能，请写出求解过程，若不能，说明理由．

    查看答案和解析>>

    同步练习册答案