
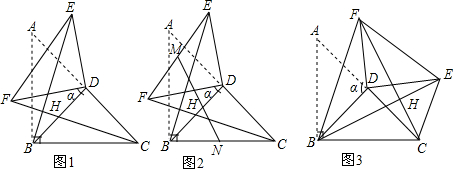
分析 (1)首先判断出BD=AD=CD,然后根据旋转的性质,判断出ED=FD,∠BDE=∠CDF;最后根据全等三角形的判定方法,判断出△BED≌△CFD,即可判断出BE=FC.
(2)首先连接BF,取BF中点G,连接MG、NG,判断出BE⊥CF;然后根据M为EF中点,G为BF中点,N为BC中点,判断出MG∥BE,MG=$\frac{1}{2}BE$,NG∥FC,NG=$\frac{1}{2}FC$;最后根据BE=FC,BE⊥FC,判断出MG=NG,∠MGN=90°,即△MGN为等腰直角三角形,即可判断出MN=$\frac{\sqrt{2}}{2}FC$.
(3)首先根据BE⊥FC,可得BF2+CE2=EF2+BC2=BH2+CH2+EH2+FH2;然后根据EF=AB,可得BF2+CE2=AB2+BC2=AC2,据此判断即可.
解答 (1)解:∵AB=BC=2,∠ABC=90°,BD为斜边AC上的中线,
∴BD=AD=CD,
又∵ED=AD,FD=BD,
∴ED=FD,
∵∠BDE=∠FDE+∠α=90°+∠α,
∠CDF=∠CDB+∠α=90°+∠α,
∴∠BDE=∠CDF,
在△BED和△CFD中,
$\left\{\begin{array}{l}{ED=FD}\\{∠BDE=∠CDF}\\{BD=CD}\end{array}\right.$
∴△BED≌△CFD,
∴BE=FC.
(2)证明:如图2,连接BF,取BF中点G,连接MG、NG,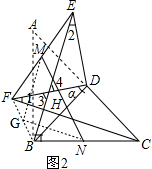 ,
,
∵△BED≌△CFD,
∴∠1=∠2,
又∵∠3=∠4,
∴∠FHE=∠FDE=90°,
∴BE⊥CF,
∵M为EF中点,G为BF中点,
∴MG∥BE,MG=$\frac{1}{2}BE$,
∵G为BF中点,N为BC中点,
∴NG∥FC,NG=$\frac{1}{2}FC$,
又∵BE=FC,BE⊥FC,
∴MG=NG,∠MGN=90°,
∴△MGN为等腰直角三角形,
∴MN=$\sqrt{2}NG=\sqrt{2}×\frac{1}{2}FC=\frac{\sqrt{2}}{2}FC$.
(3)解:由(2),可得BE⊥FC,
∴BF2=BH2+FH2,
CE2=CH2+EH2,
EF2=EH2+FH2,
BC2=BH2+CH2,
∴BF2+CE2=EF2+BC2=BH2+CH2+EH2+FH2,
∵EF=AB,
∴BF2+CE2=AB2+BC2=AC2,
∴BF2+CE2=AC2.
故答案为:BE=FC、BF2+CE2=AC2.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了全等三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.
(4)此题还考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
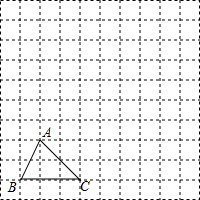 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
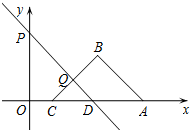 如图,在平面直角坐标系中,点A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.
如图,在平面直角坐标系中,点A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
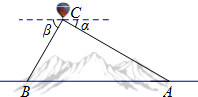 2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)
2014年11月25日,国家发改委批准了我省三条泛亚铁路的规划和建设计划.为加快勘测设计,某勘测部门使用了热气球对某隧道的长进行勘测.如图所示,热气球C的探测器显示,从热气球观测隧道入口A的俯角α为30°,观测隧道出口B的俯角β为60°,热气球相对隧道的飞行高度为1200m,求这条隧道AB的长?(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留2位小数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P、Q是反比例函数y=$\frac{k}{x}$图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1=S2.(填“>”或“<”或“=”)
如图,点P、Q是反比例函数y=$\frac{k}{x}$图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1,△QMN的面积记为S2,则S1=S2.(填“>”或“<”或“=”)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com