
【题目】如图,在![]() 中,以
中,以![]() 为直径的
为直径的![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
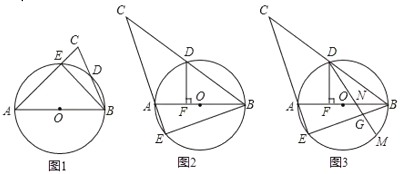
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,
如图2,![]() 为钝角时,过点
为钝角时,过点![]() 作
作![]() 于点
于点![]() 求证:
求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,在∠BDF的内部作
的条件下,在∠BDF的内部作![]() ,使
,使![]() 分别交
分别交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】某学校初一、初二年级各有500名学生,为了解两个年级的学生对消防安全知识的掌握情况,学校从初一、初二年级各随机抽取20名学生进行消防安全知识测试,满分100分,成绩整理分析过程如下,请补充完整:
(收集数据)
初一年级20名学生测试成绩统计如下:
78 56 74 81 95 75 87 70 75 90 75 79 86 60 54 80 66 69 83 97
初二年级20名学生测试成绩不低于80,但是低于90分的成绩如下:
83 86 81 87 80 81 82
(整理数据)按照如下分数段整理、描述两组样本数据:
成绩 |
|
|
|
|
|
初一 | 2 | 3 | 7 | 5 | 3 |
初二 | 0 | 4 | 5 | 7 | 4 |
(分析数据)两组样本数据的平均数、中位数、众数、方差如下表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 76.5 | 76.5 |
| 132.5 |
初二 | 79.2 |
| 74 | 100.4 |
(1)直接写出![]() ,
,![]() 的值;
的值;
(2)根据抽样调查数据,估计初一年级消防安全知识测试成绩在70分及其以上的大约有多少人?
(3)通过以上分析,你认为哪个年级对消防安全知识掌握得更好,并说明推断的合理性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边
的边![]() 在正方形
在正方形![]() 的边
的边![]() 上,连结
上,连结![]() 、
、![]() .
.
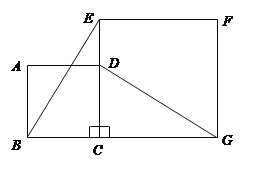
(1)观察猜想![]() 与
与![]() 之间的大小关系,并证明你的结论;
之间的大小关系,并证明你的结论;
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,说出旋转过程;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
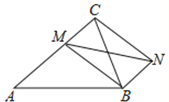
【题目】如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为![]() 两车之间的距离为
两车之间的距离为![]() ,图中的折线表示
,图中的折线表示![]() 与
与![]() 之间的函数关系,下列说法中错误的是( )
之间的函数关系,下列说法中错误的是( )
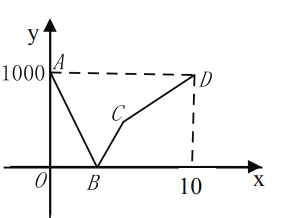
A.甲乙两地相距![]() B.点
B.点![]() 表示此时两车相遇
表示此时两车相遇
C.慢车的速度为![]() D.折线
D.折线![]() 表示慢车先加速后减速最后到达甲地
表示慢车先加速后减速最后到达甲地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】"桃花流水窅然去,别有天地非人间."桃花园景点2017年三月共接待游客![]() 万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加
万人,2018年三月比2017年三月旅游人数增加5%,已知2017年三月至2019年三月欣赏桃花的游客人数平均年增长率为8%,设2019年三月比2018年三月游客人数增加![]() ,则可列方程为( )
,则可列方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
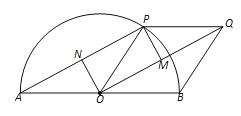
【题目】如图,已知AB为半圆O的直径,P为半圆上的一个动点(不含端点),以OP、OB为一组邻边作POBQ,连接OQ、AP,设OQ、AP的中点分别为M、N,连接PM、ON.
(1)试判断四边形OMPN的形状,并说明理由.
(2)若点P从点B出发,以每秒15°的速度,绕点O在半圆上逆时针方向运动,设运动时间为ts.
①试求:当t为何值时,四边形OMPN的面积取得最大值?并判断此时直线PQ与半圆O的位置关系(需说明理由);
②是否存在这样的t,使得点Q落在半圆O内?若存在,请直接写出t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
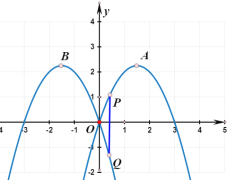
【题目】如图,在平面直角坐标系中,抛物线![]() 的解析式为
的解析式为![]() ,将抛物线
,将抛物线![]() 沿
沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() ,抛物线
,抛物线![]() 、
、![]() 的顶点分别为
的顶点分别为![]() 、
、![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,横坐标为
上一点,横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的平行线交抛物线
轴的平行线交抛物线![]() 于点
于点![]() .
.
(1)当![]() 时;
时;
①请直接写出抛物线![]() 的解析式;
的解析式;
②当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 时.
时.
①![]() 为抛物线
为抛物线![]() 上一动点,当
上一动点,当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]() 的值;
的值;
②以![]() 为边向左作正方形
为边向左作正方形![]() ,设横坐标为整数的点称为“梦想点”,当正方形
,设横坐标为整数的点称为“梦想点”,当正方形![]() 的内部(不包括边上)有6个“梦想点”时,直接写出
的内部(不包括边上)有6个“梦想点”时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com