
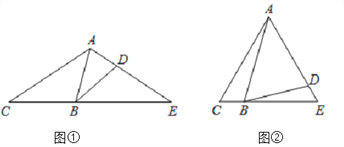
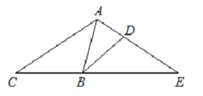
【题目】探究:如图①,△ACE中,AC=AE,点B在边CE上,点D在边AE上,∠ABD=∠E.求证:△ACB∽△BED.
应用:如图②,△ACE为等边三角形,点B在边CE上,点D在边AE上,∠ABD=60°,BC=![]() BE,则△ABD与△BDE的面积比为 .
BE,则△ABD与△BDE的面积比为 .
【答案】(1)证明见解析;(2)13:3
【解析】试题分析:(1)由等边对等角,得到∠C=∠E,由三角形外角的性质得到∠ABC=∠BDE,再由有两个角分别相等的两个三角形相似,得证;(2)由△ACB∽△BED,根据相似三角形的对应边成比例,可求得△ABC与△BDE的面积比,△ABC与△ABE的面积比,继而求得答案.
试题解析:(1)
∵AC=AE,
∴∠C=∠E,
∵∠ABC=∠∠BAE+∠E, ∠BDE=∠BAE+∠ABD, ∠ABD=∠E,
∴∠ABC=∠BDE,
在△ABC和△BDE中,
![]()
∴△ABC∽△BDE;
(2)∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,∠C=∠ABD,
∴∠CAB=∠DBE,
∵∠C=∠E=60,
∴△ACB∽△BED,
∵△ACE是等边三角形,BC=![]() BE
BE
∴△ACB与△BED的相似比为:4:3,
∴S△ABC:S△BED=16:9,S△ABC:S△ABE=1:3=16:48,
设S△ABC=16x,则S△ABE=48x,S△BDE=9x
∴S△ABD=S△ABES△BED=48x9x=39x,
∴S△ABD:S△BDE=39:9=13:3.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=![]() S△ABC,上述结论中始终正确有 ( )
S△ABC,上述结论中始终正确有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+(m-1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与x轴的交点坐标;
(3)画出这条抛物线大致图象;
(4)根据图象回答:
① 当x取什么值时,y>0 ?
② 当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
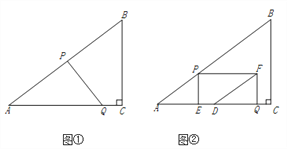
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某集团公司有9个子公司,各个子公司所创年利润的情况如下表所示.各子公司所创年利润的众数和中位数分别是( )
年利润(千万元) | 6 | 4 | 3 | 2 |
子公司个数 | 1 | 2 | 4 | 2 |
A.4千万元,3千万元
B.6千万元,4千万元
C.6千万元,3千万元
D.3千万元,3千万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王刚同学拟了一张招领启事:“今天拾到钱包一个,内有人民币8.5元,请失主到一(1)班认领”.你认为这个启事合理吗?如果不合理,问题在哪里?请你改正过来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com