
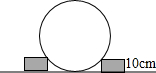
 某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程.
某公园中央地上有一个大理石球,小明想测量球的半径.于是找了两块厚10cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是60cm,聪明的你也能算出这个大石球的半径了吗?写出你的计算过程. 分析 经过圆心O作地面的垂线,垂足为C点,连接AB,交OC于点D,可得出OC与AB垂直,利用垂径定理得到D为AB的中点,由AB的长求出AD的长,设圆的半径为xcm,即OA=OC=xcm,在直角三角形AOD中,OD=OC-CD=(x-10)cm,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为这个大理石球的半径.
解答 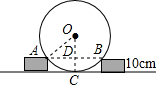 解:如图所示,过圆心O作地面的垂线OC,交地面于点C,连接AB,与OC交于点D,
解:如图所示,过圆心O作地面的垂线OC,交地面于点C,连接AB,与OC交于点D,
∵AB与地面平行,
∴OC⊥AB,
∴D为AB的中点,即AD=BD=$\frac{1}{2}$AB=30cm,又CD=10cm,
设圆的半径为xcm,则OA=OC=xcm,
∴OD=OC-CD=(x-10)cm,
在Rt△AOD中,根据勾股定理得:OA2=AD2+OD2,即x2=302+(x-10)2,
整理得:x2=900+x2-20x+100,即20x=1000,
解得:x=50,
答:这个大石球的半径是50cm.
点评 此题考查了垂径定理的应用,以及勾股定理,利用了方程的思想,结合图形构造直角三角形是解本题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+1)2 | B. | y=(x-1)2 | C. | y=x2+1 | D. | y=x2-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3×2=-5 | B. | $\root{3}{-\frac{27}{8}}$=-$\frac{3}{2}$ | C. | -5-2×(-3)=-1 | D. | (-2)3=-6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com