
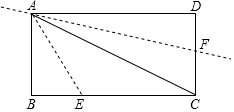
 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.
如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$. 分析 根据矩形的性质得到∠B=∠BAD=90°,根据三角函数的定义得到∠BAC=60°,根据折叠的性质得到∠BAE=∠CAE=30°,∠DAF=∠CAF,求得∠EAP=∠EAC+∠FAC=$\frac{1}{2}∠$BAD=45°,过E作EP⊥AF于P,此时,PE的值最小,解直角三角形得到AE=2$\sqrt{6}$,于是得到结论.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,
∴tan∠BAC=$\frac{BC}{AB}$=$\sqrt{3}$,
∴∠BAC=60°,
∵把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,
∴∠BAE=∠CAE=30°,∠DAF=∠CAF,
∴∠EAP=∠EAC+∠FAC=$\frac{1}{2}∠$BAD=45°,
过E作EP⊥AF于P,
此时,PE的值最小,
∵AB=3$\sqrt{2}$,∠B=90°,∠BAE=30°,
∴AE=2$\sqrt{6}$,
∵∠APE=90°,∠EAP=45°,
∴PE=$\frac{\sqrt{2}}{2}$AE=2$\sqrt{3}$.
∴PE的最小值为2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,解直角三角形,等腰直角三角形的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:选择题
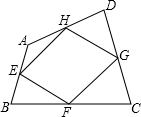 如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )
如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )| A. | 一定不是平行四边形 | B. | 一定不是中心对称图形 | ||
| C. | 可能是轴对称图形 | D. | 当AC=BD时它是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
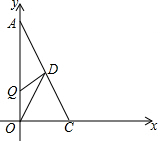 如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.
如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足$\sqrt{a-2b}$+|b-2|=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
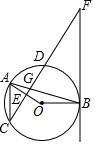 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.
如图,在9×8的正方形的网格中,△ABC的三个顶点和点O都在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
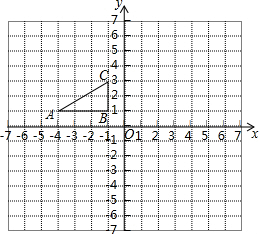 如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
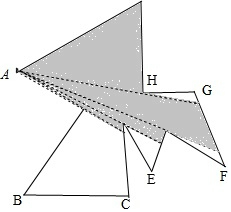 如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )
如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )| A. | E处 | B. | F处 | C. | G处 | D. | H处 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13或17 | B. | 13 | C. | 17 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com