
【题目】如图,已知在平面直角坐标系xOy中,二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),且与y轴相交于点C.
(1)求这个二次函数的解析式并写出其图象顶点D的坐标;
(2)求∠CAD的正弦值;
(3)设点P在线段DC的延长线上,且∠PAO=∠CAD,求点P的坐标.

【答案】(1)y=﹣x2+2x+3,顶点D(1,4);(2)![]() ;(3)(
;(3)(![]() ,
,![]() ),(﹣6,﹣3).
),(﹣6,﹣3).
【解析】
试题分析:(1)根据二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),求得m和n的值即可;
(2)根据A,C,D三点的坐标,求得CD=![]() ,AC=
,AC=![]() ,AD=
,AD=![]() ,得到CD2+AC2=AD2,根据勾股定理的逆定理得出△ACD是直角三角形,且∠ACD=90°,据此求得∠CAD的正弦值;
,得到CD2+AC2=AD2,根据勾股定理的逆定理得出△ACD是直角三角形,且∠ACD=90°,据此求得∠CAD的正弦值;
(3)先求得直线CD为y=x+3,再设点P的坐标为(a,a+3),然后分两种情况进行讨论:当点P在x轴上方时,过点P作PE⊥x轴于E;当点P在x轴下方时,过点P作PF⊥x轴于F,分别判定△ACD∽△AEP,△ACD∽△AFP,列出比例式求得a的值即可.
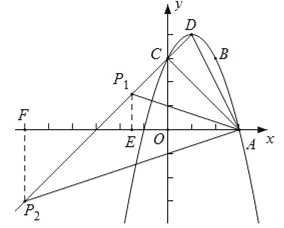
试题解析:(1)∵二次函数y=﹣x2+mx+n的图象经过点A(3,0),B(m,m+1),∴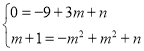 ,解得:
,解得:![]() ,∴二次函数的解析式为:y=﹣x2+2x+3,顶点D的坐标为(1,4);
,∴二次函数的解析式为:y=﹣x2+2x+3,顶点D的坐标为(1,4);
(2)如图所示,在y=﹣x2+2x+3中,当x=0时,y=3,∴C(0,3).
∵A(3,0),D(1,4),∴CD=![]() ,AC=
,AC=![]() ,AD=
,AD=![]() ,∴CD2+AC2=AD2,∴△ACD是直角三角形,且∠ACD=90°,∴sin∠ACD=
,∴CD2+AC2=AD2,∴△ACD是直角三角形,且∠ACD=90°,∴sin∠ACD=![]() =
=![]() ;
;
(3)∵直线CD经过C(0,3),D(1,4),∴设可设直线CD为y=kx+b,则
![]() ,解得:
,解得:![]() ,∴直线CD为y=x+3,设点P的坐标为(a,a+3),①如图所示,当点P在x轴上方时,过点P作PE⊥x轴于E,则
,∴直线CD为y=x+3,设点P的坐标为(a,a+3),①如图所示,当点P在x轴上方时,过点P作PE⊥x轴于E,则
PE=a+3,AE=3﹣a,∵∠AEP=∠ACD=90°,∠PAO=∠CAD,∴△ACD∽△AEP,∴![]() ,即
,即![]() ,解得a=
,解得a=![]() ,∴a+3=
,∴a+3=![]() ,∴此时P的坐标为(
,∴此时P的坐标为(![]() ,
,![]() );
);
②如图所示,当点P在x轴下方时,过点P作PF⊥x轴于F,则
PF=﹣(a+3),AF=3﹣a,∵∠AFP=∠ACD=90°,∠PAO=∠CAD,∴△ACD∽△AFP,∴![]() ,即
,即![]() ,解得a=﹣6,∴a+3=﹣3,∴此时P的坐标为(﹣6,﹣3);
,解得a=﹣6,∴a+3=﹣3,∴此时P的坐标为(﹣6,﹣3);
综上所述,点P的坐标为(![]() ,
,![]() ),(﹣6,﹣3).
),(﹣6,﹣3).


科目:初中数学 来源: 题型:
【题目】如图,因为AB∥CD(已知),所以∠BEF=∠CFE(两直线平行,) 因为EG平分∠BEF,FH平分∠CFE(已知),
所以∠2= ![]() ∠BEF,∠3=()
∠BEF,∠3=()
所以∠2=(等量代换),
所以EG∥( , 两直线平行).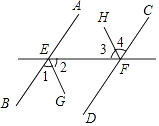
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证安全,某仓库引进A型、B型两台机器人搬运某种有毒货物到仓库存放,这两台机器人充满电后,各能连续工作5h,按照指令,A型机器人于某日零时开始搬运,过了1h,B型机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(kg)与A型机器人搬运时间x(h)之间的关系图象,线段EF表示B种机器人的搬运量yB(kg)与A型机器人的时间x(h)之间的关系图象,根据图象提供的信息解答下列问题: 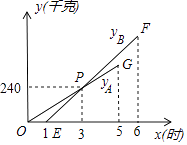
(1)点P表示的意义为:当x=3h时
(2)直接写出线段OG所表示的搬运量与时间x(h)之间的关系式
(3)A型机器人每小时搬运有毒货物kg,B型机器人每小时搬运有毒货物kg.
(4)到工作结束(各5h),A型、B型两台机器人共搬运多少有毒货物?
查看答案和解析>>
科目:初中数学 来源: 题型:
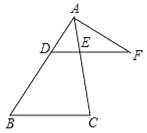
【题目】如图,在△ABC中,点D是AB边上一点,过点D作DE∥BC,交AC于E,点F是DE延长线上一点,联结AF.
(1)如果![]() ,DE=6,求边BC的长;
,DE=6,求边BC的长;
(2)如果∠FAE=∠B,FA=6,FE=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF.其中正确结论的个数是( )
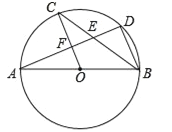
A.2 B.3 C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com