
【题目】山西省地处中纬度,属于温带大陆性气候,因此适合种植玉米、高粱、大豆、花生等农作物,农民李大叔有一块总面积为![]() 的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:


农作物 | 占地面积( | 产量(千克/垄) | 利润(元/千克) |
玉米 | 30 | 60 | 0.5 |
高粱 | 20 | 50 | 0.8 |
(1)若设高粱种植了![]() 垄,请说明共有几种种植方案,分别是哪几种;
垄,请说明共有几种种植方案,分别是哪几种;
(2)在以上种植方案中,哪种方案获得的利润最大?最大利润是多少?
【答案】(1)共有三种种植方案:方案一:种植高粱16垄,种植玉米16垄;方案二:种植高粱17垄,种植玉米15垄;方案三:种植高粱18垄,种植玉米14垄;(2)方案三获得的利润最大,最大利润是1140元.
【解析】
(1)高粱种植了![]() 垄,则玉米种了
垄,则玉米种了![]() 垄,根据总面积小于等于800m2,单种农作物的垄数不低于14垄,又不超过18垄,建立不等式即可确定
垄,根据总面积小于等于800m2,单种农作物的垄数不低于14垄,又不超过18垄,建立不等式即可确定![]() 的取值范围,从而得出方案;
的取值范围,从而得出方案;
(2)分别计算出(1)中种植方案的利润,进行比较即可得出答案.
解:(1)根据题意可知:玉米种了![]() 垄,
垄,
则 ,且
,且![]() 是正整数,
是正整数,
解得![]() ,且
,且![]() 是正整数,
是正整数,
∴![]() 的值为16,17,18.
的值为16,17,18.
故共有三种种植方案:
方案一:种植高粱16垄,种植玉米16垄;
方案二:种植高粱17垄,种植玉米15垄;
方案三:种植高粱18垄,种植玉米14垄.
(2)方案一获得的利润为:![]() (元);
(元);
方案二获得的利润为:![]() (元);
(元);
方案三获得的利润为:![]() (元).
(元).
由计算可知,方案三:即种植高粱18垄,种植玉米14垄,获得的利润最大,最大利润是1140元.


科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
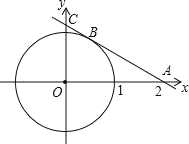
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
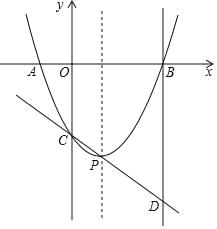
【题目】如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB=![]() .
.
(1)则 A、B 两点的坐标分别为 A( , ); B( , );
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
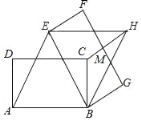
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节期间,南部山区某果园平均每天可卖出 300 斤核桃 ,卖出 1 斤核桃的利润是 1 元,经调查发现,零售单价每降 0.1 元,每天可多卖出 100 斤.设该店决定把零售单价下降 x(0<x<1)元.
(1)零售单价下降 x 元后,该店平均每天可卖出多少斤核桃(用 含出 x 的代数式表示,需要简化);
(2)在不考虑其他国素的条件下,为了薄利多销,当零售单价下降多少时,才能使该店每天获取的利润是 420元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com