
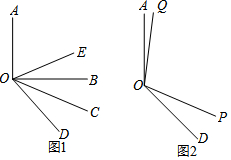
分析 (1)①由图和题意知∠EOC=$\frac{1}{2}$∠AOD-$\frac{1}{2}$∠BOD,代入计算即可.
②由图和题意知∠EOC=$\frac{1}{2}$(∠AOB+∠BOD)-$\frac{1}{2}$∠BOD,代入计算即可.
(2)由题意知,有两种情况,①当OQ在OP左侧,②当OQ在OP右侧时,列出关于多少秒,∠POQ=$\frac{1}{2}$∠AOQ的方程,解方程即可.
解答 解:(1)①∵∠AOB=90°,∠DOB=30°,
∴∠AOD=∠AOB+∠BOD=120°,
∵射线OC平分∠DOB,射线OE平分∠AOD,
∴∠EOD=$\frac{1}{2}∠$AOD=60°,∠COD=$\frac{1}{2}$∠DOB=15°,
∴∠EOC=∠EOD-∠COD=45°;
②∵∠AOB=β,∠DOB=α,
∴∠AOD=∠AOB+∠BOD=β+α,
∵射线OC平分∠DOB,射线OE平分∠AOD,
∴∠EOD=$\frac{1}{2}∠$AOD=$\frac{1}{2}$(α+β),∠COD=$\frac{1}{2}$∠DOB=$\frac{1}{2}$α,
∴∠EOC=∠EOD-∠COD=$\frac{1}{2}$β;
(2)分为两种情况:
情况①当OQ在OP左侧,t秒后∠POQ=$\frac{1}{2}$∠AOQ,
此时120-(5t+15t)=$\frac{1}{2}$×5t
解得t=$\frac{48}{9}$;
情况②当OQ在OP右侧时,m秒后∠POQ=$\frac{1}{2}$∠AOQ,
此时5m-[(m-$\frac{120}{15}$)×15]=$\frac{5m}{2}$
解得:m=$\frac{48}{5}$
答:当过了$\frac{48}{9}$秒和$\frac{48}{5}$秒时,∠POQ=$\frac{1}{2}$∠AOQ.
点评 本题考查了角平分线的性质、角的和差关系及列方程解实际问题.解决本题的关键是看懂图,分好类,列出关于时间的方程.


科目:初中数学 来源: 题型:填空题
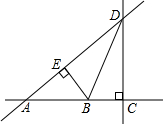 如图所示,直线AD与直线BD相交于点D,BE⊥AD垂足为点E,点B到直线AD的距离是线段BE的长度,点D到直线AB的距离是线段DC的长度.
如图所示,直线AD与直线BD相交于点D,BE⊥AD垂足为点E,点B到直线AD的距离是线段BE的长度,点D到直线AB的距离是线段DC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
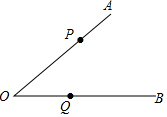 已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图
已知点P、Q分别在∠ACB的边OA、OB上,按下列要求画图查看答案和解析>>
科目:初中数学 来源: 题型:填空题
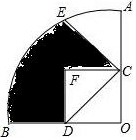 如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.
如图,在圆心角为90°的扇形AOB中,半径OA=2,点C、D分别是OA、OB的中点,点E是$\widehat{AB}$的一个三等分点,将△COD沿CD折叠,点O落在点F处,则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com