
分析 (1)分两种情况:①分子<0,分母>0;②分子>0,分母<0;进行讨论即可求解;
(2)先因式分解,再根据一元二次不等式的解法求解即可;
(3)先因式分解,再根据一元二次不等式的解法求解即可.
解答 解:(1)$\frac{x+2}{x-4}$≤0,
①分子≤0,分母>0,则$\left\{\begin{array}{l}{x+2≤0}\\{x-4>0}\end{array}\right.$,无解;
②分子≥0,分母<0,则$\left\{\begin{array}{l}{x+2≥0}\\{x-4<0}\end{array}\right.$,解得-2≤x<4.
故$\frac{x+2}{x-4}$≤0的解集为-2≤x<4;
(2)(2x-1)2+(x-1)2≥x,
4x2-4x+1+x2-2x+1≥x,
5x2-7x+2≥0,
(5x-2)(x-1)≥0,
故(2x-1)2+(x-1)2≥x的解集为x≤$\frac{2}{5}$或x≥1;
(3)x2-(a+1)x+a≤0,
(x-1)(x-a)≤0,
故x2-(a+1)x+a≤0的解集为1≤x≤a(a≥1),a≤x≤1(a≤1).
点评 此题考查了一元二次不等式,解一元二次不等式,可将一元二次不等式不等式转化成二次函数的形式,求出函数与X轴的交点,将一元二次不等式,二次函数,一元二次方程联系起来,并利用图象法进行解题,使得问题简化.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
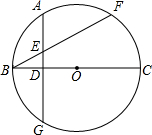 已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.
已知:如图,BC为⊙O的直径,BF为弦,A为$\widehat{BF}$的中点,AD⊥BC,垂足为D,AD和BF相交于点E,求证:AE=BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com