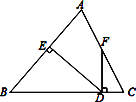
【题目】如图所示，△ABC中，AB=BC，DE⊥AB于点E，DF⊥BC于点D，交AC于F．
⑴若∠AFD=155°，求∠EDF的度数；
⑵若点F是AC的中点，求证：∠CFD=
∠B．
【答案】（1）50°；（2）见解析
【解析】试题分析：⑴根据等腰三角形的性质、三角形的内角和定理与四边形的内角和为360°，可求得所求角的度数.
⑵连接BF，根据三角形内角和定理与等腰三角形三线合一，可知
.
试题解析：⑴ ∵∠AFD=155°，∴∠DFC=25°，∵DF⊥BC，DE⊥AB，
∴∠FDC=∠AED=90°，
在Rt△EDC中，∴∠C=90°﹣25°=65°，
∵AB=BC，∴∠C=∠A=65°，
∴∠EDF=360°﹣65°﹣155°﹣90°=50°．
⑵ 连接BF，∵AB=BC，且点F是AC的中点，
∴BF⊥AC，
，
∴∠CFD+∠BFD=90°，∠CBF+∠BFD=90°，
∴∠CFD=∠CBF，
∴．
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，二次函数y=（x-a）（x-3）（0<a<3）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点D，过其顶点C作直线CP⊥x轴，垂足为点P，连接AD、BC.
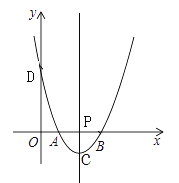
（1）求点A、B、D的坐标；
（2）若△AOD与△BPC相似，求a的值；
（3）点D、O、C、B能否在同一个圆上，若能，求出a的值，若不能，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l1∥l2∥l3，等腰直角三角形ABC的三个顶点A，B，C分别在l1，l2，l3上，∠ACB=90°，AC交l2于点D，已知l1与l2的距离为1，l2与l3的距离为3，则
的值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，∠BAC＝90°，AB＝AC，D 是 AC 边上一动点， CE⊥BD 于 E．
(1)如图（1），若 BD 平分∠ABC 时，①求∠ECD 的度数；②求证：BD＝2EC；
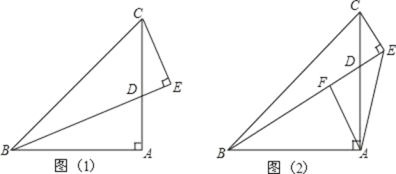
(2)如图（2），过点 A 作 AF⊥BE 于点 F，猜想线段 BE，CE，AF 之间的数量关系并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
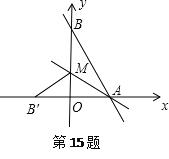
【题目】如图，直线y=﹣
x+8与x轴，y轴分别交于点A和B，M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B′处，则直线AM的解析式为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的三分线，在△ABC中，∠B＝30°，AD和 DE是△ABC的三分线，点D在 BC 边上，点E在 AC边上，且AD＝BD，DE＝CE，请写出∠C所有可能的度数________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
