
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于P(n,2),与x轴交于A(﹣4,0),与y轴交于C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于P(n,2),与x轴交于A(﹣4,0),与y轴交于C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象有一点D,使得以B、C、P、D为顶点的四边形是菱形,求出点D的坐标.
【答案】
(1)
解:∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得: ![]() ,
,
解得:k= ![]() ,b=1,
,b=1,
∴一次函数解析式为y= ![]() x+1,
x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y= ![]()
(2)
解:如图所示,
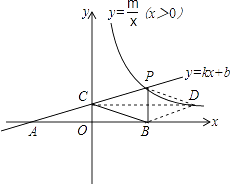
当PB为菱形的对角线时,
∵四边形BCPD为菱形,
∴PB垂直且平分CD,
∵PB⊥x轴,P(4,2),
∴点D(8,1).
当PC为菱形的对角线时,PB∥CD,
此时点D在y轴上,不可能在反比例函数的图象上,故此种情形不存在.
综上所述,点D(8,1).
【解析】(1)先根据题意得出P点坐标,再将A、P两点的坐标代入y=kx+b求出kb的值,故可得出一次函数的解析式,把点P(4,2)代入反比例函数y= ![]() 即可得出m的值,进而得出结论;(2)根据PB为菱形的对角线与PC为菱形的对角线两种情况进行讨论即可.
即可得出m的值,进而得出结论;(2)根据PB为菱形的对角线与PC为菱形的对角线两种情况进行讨论即可.
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和菱形的性质的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.


科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( )
(k≠0)上,AB∥x轴,分别过点A,B向x轴作垂线,垂足分别为D,C,若矩形ABCD的面积是8,则k的值为( ) 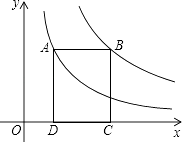
A.12
B.10
C.8
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 ![]() =
= ![]() =
= ![]() .
. 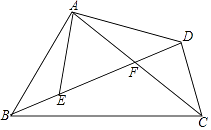
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题: A、B两地的距离是80公里,一辆公共汽车从A地驶出3小时后,一辆小汽车也从A地出发,它的速度是公共汽车的3倍,已知小汽车比公共汽车迟20分钟到达B地,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB= ![]() ,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为(结果保留π).
,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰好在弧EF上,则图中阴影部分的面积为(结果保留π). 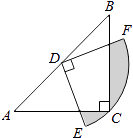
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90° 
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com