Question

7．如图1，B、D分别是x轴和y轴的正半轴上的点，AD∥x轴，AB∥y轴（AD＞AB），点P从C点出发，以3cm/s的速度沿C-D-A-B匀速运动，运动到B点时终止；点Q从B点出发，以2cm/s的速度，沿B-C-D匀速运动，运动到D点时终止．P、Q两点同时出发，设运动的时间为t（s），△PCQ的面积为S（cm²），S与t之间的函数关系由图2中的曲线段OE，线段EF、FG表示．
（1）求A、D点的坐标；
（2）求图2中线段FG的函数关系式；
（3）是否存在这样的时间t，使得△PCQ为等腰三角形？若存在，直接写出t的值；若不存在，请说明理由．

Answer 1

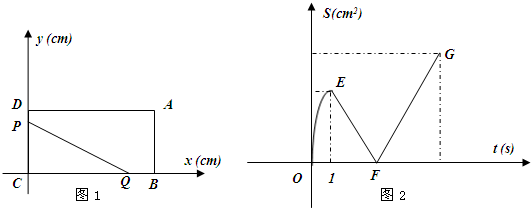
分析 （1）由图象可知CD=3×1=3，设AD=BC=a，根据点Q到达点C时，点P到达点A，列出方程即可求出a．
（2）当点Q在CD上，点P在AB上时，对应的函数图象是线段FG，由此即可解决问题．
（3）分三种情形讨论：①Q在BC上，P在CD上时，列出方程即可，②Q在BC上，P在AD上时，由CP=CQ得6-2t=$\sqrt{{3}^{2}+（3t-3）^{2}}$，整理得5t²+6t+54=0，△＜0无解．
由PQ=CQ得$\sqrt{{3}^{2}+（9-5t）^{2}}$=6-2t，整理得7t²-22t+18=0，△＜0，无解．当PC=PQ得6-2t=2（3t-3），解得t=$\frac{3}{2}$，
③Q在CD上，P在AB上时，由CP=PQ列出方程即可．

解答 解：（1）设AD=BC=a，
由图象可知CD=AB=3，点Q到达点C时，点P到达点A，
∴$\frac{a}{3}$=$\frac{a-3}{2}$，
∴a=6，
∴点A坐标（6，3），点D坐标（0，3）．
（2）当点Q在CD上，点P在AB上时，对应的函数图象是线段FG，
∴S=$\frac{1}{2}$•PC•6=3PC=3（（2t-6）=6t-18．
（3）①Q在BC上，P在CD上时，由CP=CQ得6-2t=3t，解得t=$\frac{6}{5}$（不合题意舍弃，$\frac{6}{5}$＞1），
②Q在BC上，P在AD上时，
由CP=CQ得6-2t=$\sqrt{{3}^{2}+（3t-3）^{2}}$，
整理得5t²+6t+54=0，△＜0无解．
由PQ=CQ，如图1中，

作PK⊥OB于K，则DP=OK=3t-3，KQ=6-2t-（3t-3）=9-5t，
∴PQ=$\sqrt{P{K}^{2}+K{Q}^{2}}$=$\sqrt{{3}^{2}+（9-5t）^{2}}$
∴$\sqrt{{3}^{2}+（9-5t）^{2}}$=6-2t，
整理得7t²-22t+18=0，△＜0，无解．
当PC=PQ．如图2中，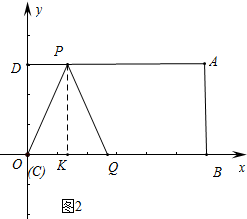

作PK⊥OB于K，则OK=KQ=DP，
∴OQ=2DP，
∴6-2t=2（3t-3），解得t=$\frac{3}{2}$，
③Q在CD上，P在AB上时，由CP=PQ，
如图3中，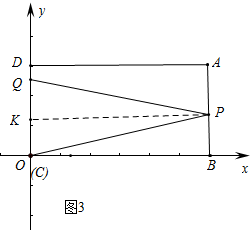

作PK⊥OD于K，则KQ=OK=PB，
∴2PB=OQ，
∴2（12-3t）=2t-6，解得t=$\frac{15}{4}$，
综上所述t=$\frac{3}{2}$s或$\frac{15}{4}$s时，△PCQ为等腰三角形是等腰三角形．

点评 本题考查三角形综合题、勾股定理、等腰三角形的大盘会选择等知识，解题的关键是读懂图象信息，学会构建方程解决问题，属于中考常考题型．