
如图,ABCD为平行四边形,AD=a,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:DF=FE;
(2)若AC=2CF,![]() ,AC⊥DC,求BE的长;
,AC⊥DC,求BE的长;
(3)在(2)的条件下,求四边形ABED的面积.

(1)证明:延长DC交BE于点M,∵BE∥AC,AB∥DC,∴四边形ABMC是平行四边形,
∴CM=AB=DC,C为DM的中点,BE∥AC,DF=FE;
(2)解:由(2)得CF是△DME的中位线,
故ME=2CF,又∵AC=2CF,四边形ABMC是平行四边形,
∴BE=2BM=2ME=2AC, 又∵AC⊥DC,
∴在Rt△ADC中利用勾股定理得AC=![]() , ∴=
, ∴=![]() .
.
(3)可将四边形ABED的面积分为两部分,梯形ABMD和三角形DME,
在Rt△ADC中利用勾股定理得DC=![]() ,
,
由CF是△DME的中位线得CM=DC=![]() ,
,
四边形ABMC是平行四边形得AM=MC=![]() ,BM=AC=
,BM=AC=![]() ,
,
∴梯形ABMD面积为:![]()
![]() ;
;
由AC⊥DC和BE∥AC可证得三角形DME是直角三角形,
其面积为:![]() ,∴四边形ABED的面积为
,∴四边形ABED的面积为![]() +
+![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
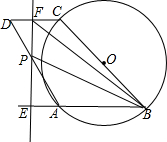 如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.
如图,ABCD为平行四边形,以BC为直径的⊙O经过点A,∠D=60°,BC=2,一动点P在AD上移动,过点P作直线AB的垂线,分别交直线AB、CD于E、F,设点O到EF的距离为t,若B、P、F三点能构成三角形,设此时△BPF的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
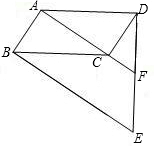 如图,ABCD为平行四边形,BE∥AC,DE交AC延长线于F点,交BE于E点.
如图,ABCD为平行四边形,BE∥AC,DE交AC延长线于F点,交BE于E点.| 2 |
| 5 |
| 10 |
查看答案和解析>>
科目:初中数学 来源:2011—2012学年山东潍坊八年级下期末模拟数学试卷(带解析) 题型:解答题
如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE于E点.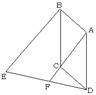
(1)求证:EF=DF;
(2)若AC=2CF,∠ADC=60 o, AC⊥DC,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东潍坊八年级下期末模拟数学试卷(解析版) 题型:解答题
如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE于E点.

(1)求证:EF=DF;
(2)若AC=2CF,∠ADC=60 o, AC⊥DC,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com