
����Ŀ��ֱ��AB��CD����P����ƽ����֮�䣬��E. F�ֱ���AB��CD�ϣ�����PE��PF.����̽�������
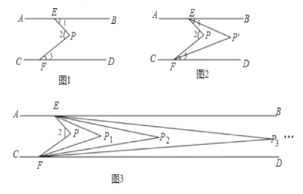
(1)��ͼ1�С�1=36��,��2=63�������3=___��
(2)̽��ͼ1�С�1����2���3֮���������ϵ����˵�����ɣ�
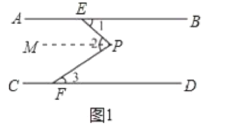
(3)��ͼ2��ʾ,��1���3��ƽ���߽��ڵ�P`,����2=��,�����EP`F�Ķ���(�ú����Ĵ���ʽ��ʾ)��
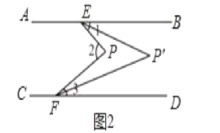
��4����ͼ3��ʾ,��ͼ2�Ļ�����,����BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ,��BEP
,��BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ����BEP
����BEP![]() ���DFP
���DFP![]() ��ƽ���߽��ڵ�P
��ƽ���߽��ڵ�P![]() ,�ҡ�2=��,ֱ��д����EP
,�ҡ�2=��,ֱ��д����EP![]() F�Ķ���(�ú����Ĵ���ʽ��ʾ).
F�Ķ���(�ú����Ĵ���ʽ��ʾ).
���𰸡���1��27������2����2=��1+��3����3��![]() ������4��
������4��![]() ����
����
��������
��1�����ý��ۣ���2=��1+��3���㼴�ɣ�
��2�����ۣ���2=��1+��3����ͼ1�У���PM��AB������ƽ���ߵ�����֤�����ɣ�
��3�����ã�2���н����Լ���ƽ���ߵĶ��弴�ɽ�����⣮
��4��̽�����ɣ����ù��ɽ�����⼴�ɣ�
(1)��3=��2��1=63��36��=27��.
�ʴ�Ϊ27��.
(2)���ۣ���2=��1+��3.
���ɣ���ͼ1��,��PM��AB.
��AB��CD,AB��PM��
��PM��CD��
���1=��MPE����3=��MPF��
���2=��1+��3.
(3)��ͼ2�У�
�ߡ�BEP+��DFP=��2=����
���EP��F=��BEP��+��DFP��=![]() (��BEP+��DFP)=
(��BEP+��DFP)=![]() ��.
��.
��4����ͼ3�У�
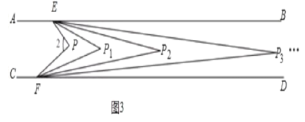
�ɣ�3����֪����P![]() =
=![]() ��,��P
��,��P![]() =(
=(![]() )
)![]() ��,��P
��,��P![]() =(
=(![]() )
)![]() ��,��,��P
��,��,��P![]() =
=![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=3x2+1��y=3��x��1��2 �� ����˵���� �����ǵ�ͼ���ǿ������ϣ�
�����ǵĶԳ��ᶼ��y�ᣬ�������궼��ԭ�㣨0��0����
�۵�x��0ʱ�����ǵĺ���ֵy��������x�����������
�����ǵĿ��ڵĴ�С��һ���ģ�
������ȷ��˵���У� ��
A. 1�� B. 2 C. 3 D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() ��
��![]() ����ȷ����C�����꣬ʹ����A��B��C��OΪ������ı�����ƽ���ı��Σ����������������е�C��������___________��
����ȷ����C�����꣬ʹ����A��B��C��OΪ������ı�����ƽ���ı��Σ����������������е�C��������___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ����P�Ӷ���B��������B��C��A��ÿ��1cm���ٶ������˶���A�㣬���˶�ʱ��Ϊx�룬
����P�Ӷ���B��������B��C��A��ÿ��1cm���ٶ������˶���A�㣬���˶�ʱ��Ϊx�룬![]() ����Ϊy cm��ijѧϰС��Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽�������������ǵ�̽�����̣��벹��������
����Ϊy cm��ijѧϰС��Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽�������������ǵ�̽�����̣��벹��������


��1��ͨ��ȡ������ͼ���������õ���x���룩��y��cm���ļ����Ӧֵ��
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.2 | 3.6 | 3.2 | 3.0 | 3.6 | 4.2 | 5.0 |
Ҫ��ȫ�����������ֵ������һλС������
��2����ƽ��ֱ������ϵ�У�����Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����ϻ����ĺ���ͼ������⣺��xԼΪ__________ʱ��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ![]() �е�ͼ��M�͵�P����P��M�ڲ���M�ϣ����������¶��壺
�е�ͼ��M�͵�P����P��M�ڲ���M�ϣ����������¶��壺
���ͼ��M�ϴ��ڵ�Q��ʹ��![]() ����ô�Ƶ�PΪͼ��M�ĺ�г�㣮
����ô�Ƶ�PΪͼ��M�ĺ�г�㣮
��֪��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1���ڵ�![]() ��
��![]() ��
��![]() ������
�У�����![]() �ĺ�г����_________________��
�ĺ�г����_________________��
��2�����ֱ��![]() �ϴ��ھ���
�ϴ��ھ���![]() �ĺ�г��P�������P�ĺ�����t��ȡֵ��Χ��
�ĺ�г��P�������P�ĺ�����t��ȡֵ��Χ��
��3�����ֱ��![]() �ϴ��ھ���
�ϴ��ھ���![]() �ĺ�г��E��F��ʹ���߶�
�ĺ�г��E��F��ʹ���߶�![]() �ϵ����е㣨���˵㣩���Ǿ���
�ϵ����е㣨���˵㣩���Ǿ���![]() �ĺ�г�㣬��
�ĺ�г�㣬��![]() �����b��ȡֵ��Χ��
�����b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��AC��CD��BE�ֱ��ǡ�ABC�Ľ�ƽ���ߣ�AG��BC��AG��BG�����н��ۣ��١�BAG��2��ABF����BAƽ�֡�CBG���ۡ�ABG����ACB���ܡ�CFB��135����������ȷ�Ľ����У���������
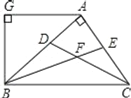
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬ij�̳����Żݴ����������ɹ˿ͳ齱ȷ���ۿۣ�ij�˿���ס���������Ʒ���ֱ�鵽���ۣ����ۼ۵�70%���ۣ��;��ۣ����ۼ۵�90%���ۣ���������386Ԫ����������Ʒԭ���ۼ�֮��Ϊ500Ԫ���ʣ���������Ʒ��ԭ���ۼ۷ֱ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����
��1����ͼ1���ڡ�ABC�У���A��40������ABC���ڽ�ƽ���߽��ڵ�P�����P�Ķ�����
��2����ͼ2���ڡ�ABC�У���A��90����BP��BQ���ȷ֡�ABC��CP��CQ���ȷ֡�ACB������PQ�����BQP�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ�����ɫ��ͬ�ĺ���ͺ�������һ�������Ĵ�����װ��4�������6������.
��1�����ȴӴ�����ȡ��m�������Żأ����ٴӴ������������һ������������������Ϊ�¼�A. ���¼�AΪ��Ȼ�¼�����m= .
��2�����ȴӴ�����ȡ��n�������ٷ���2n���������������һ�����Ǻ���ĸ��ʵ���2/3��ͨ��������n��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com