
分析 (1)本题主要是利用换元法降次来达到把一元四次方程转化为一元二次方程,来求解,然后再解这个一元二次方程.
(2)利用题中给出的方法先把x2+x当成一个整体y来计算,求出y的值,再解一元二次方程.
(3)设|x|=y,原方程可化为y2-3y-18=0,求出y的值,再解绝对值方程.
解答 解:(1)在由原方程得到方程①的过程中,利用 换元法达到 降次的目的,体现了数学的转化思想.
故答案是:换元 降次;
(2)设x2+x=y,原方程可化为y2-4y-12=0,
解得y1=6,y2=-2.
由x2+x=6,得x1=-3,x2=2.
由x2+x=-2,得方程x2+x+2=0,
b2-4ac=1-4×2=-7<0,此时方程无解.
所以原方程的解为x1=-3,x2=2.
(3)原方程可化为|x|2-3|x|-18=0,
设|x|=y,原方程可化为y2-3y-18=0,
解得y1=6,y2=-3.
由|x|=6,得x1=-6,x2=6.
由|x|=-3,此时方程无解.
所以原方程的解为x1=-6,x2=6.
点评 本题应用了换元法,把关于x的方程转化为关于y的方程,这样书写简便且形象直观,并且把方程化繁为简化难为易,解起来更方便.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
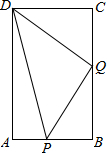 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28cm2?若存在,请求出t的值;若不存在,请说明理由.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止.问:是否存在这样的时刻,使S△DPQ=28cm2?若存在,请求出t的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的坐标为( )| A. | (3,3) | B. | (1,4) | C. | (3,1) | D. | (4,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com