

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2014届浙江绍兴杨汛桥中学七年级下学期期中考试数学试卷(解析版) 题型:解答题
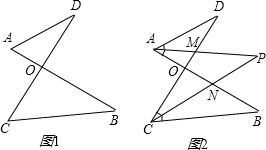
已知如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”. 那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:
1.在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;

2.仔细观察,在图2中“8”字形”的个数 个;
3.在图2中,若∠D=400,∠B=360,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;

4.如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com