
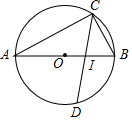
 已知△ABC是⊙O的内接三角形,AB为直径,AC=12,BC=5,CD平分∠ACB角⊙O于D,I为△ABC的内心,则DI的长度为( )
已知△ABC是⊙O的内接三角形,AB为直径,AC=12,BC=5,CD平分∠ACB角⊙O于D,I为△ABC的内心,则DI的长度为( )| A. | $\frac{13}{2}$ | B. | $\frac{13\sqrt{2}}{2}$ | C. | $\frac{13\sqrt{3}}{2}$ | D. | $\frac{15}{2}$ |
分析 如图,连接AD、BD,AI.先求出AD,再证明DI=DA即可解决问题.
解答 解:如图,连接AD、BD,AI.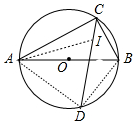
∵AB是直径,
∴∠ACB=90°,
∵AC=2,BC=5,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵∠ACD=∠DCB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴AD=BD=$\frac{13\sqrt{2}}{2}$,∠ADB=90°,
∴∠DAB=∠ACD=45°
∵I是内心,
∴∠IAC=∠IAB,
∵∠AID=∠ACD+∠CAI=45°+∠CAI,∠IAD=∠IAB+∠DAB=∠IAB+45°,
∴∠DAI=∠DIA,
∴ID=AD=$\frac{13\sqrt{2}}{2}$,
故选B.
点评 本题考查三角形的外接圆与外心,三角形的内切圆与内心,等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,判断DI=DA是突破点,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x(x-1)}{x-2}$ | B. | $\frac{x(x-2)}{x-1}$ | C. | $\frac{x-2}{x(x-1)}$ | D. | $\frac{x-1}{x(x-2)}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1、-2 | B. | -2、-1 | C. | 2、-1 | D. | -1、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{4}$ | B. | -$\frac{7}{11}$ | C. | $\sqrt{2}$ | D. | $\root{3}{-125}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com