
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. 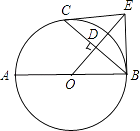
(1)求证:BE与⊙O相切;
(2)连接AD并延长交BE于点F,若OB=9,sin∠ABC= ![]() ,求BF的长.
,求BF的长.
【答案】
(1)证明:连接OC,
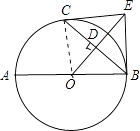
∵OD⊥BC,
∴∠COE=∠BOE,
在△OCE和△OBE中,
∵ 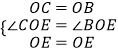 ,
,
∴△OCE≌△OBE,
∴∠OBE=∠OCE=90°,即OB⊥BE,
∵OB是⊙O半径,
∴BE与⊙O相切.
(2)解:过点D作DH⊥AB,连接AD并延长交BE于点F,
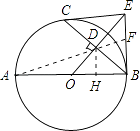
∵∠DOH=∠BOD,∠DHO=∠BDO=90°,
∴△ODH∽△OBD,
∴ ![]()
又∵sin∠ABC= ![]() ,OB=9,
,OB=9,
∴OD=6,
易得∠ABC=∠ODH,
∴sin∠ODH= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴OH=4,
∴DH= ![]() =2
=2 ![]() ,
,
又∵△ADH∽△AFB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴FB= ![]()
【解析】(1)连接OC,先证明△OCE≌△OBE,得出EB⊥OB,从而可证得结论.(2)过点D作DH⊥AB,根据sin∠ABC= ![]() ,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.
,可求出OD=6,OH=4,HB=5,然后由△ADH∽△AFB,利用相似三角形的性质得出比例式即可解出BF的长.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系. 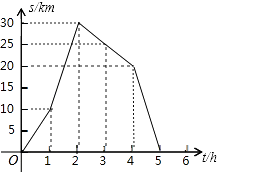
(1)在这个变化过程中自变量是 , 因变量是 .
(2)小李何时到达离家最远的地方?此时离家多远?
(3)分别求出在1≤t≤2时和2≤t≤4时小李骑自行车的速度.
(4)请直接写出小李何时与家相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
(1)求BD的长;
(2)若△DCN的面积为2,求四边形ABCM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班开展安全知识竞赛活动,班长将所有同学的成绩(得分为整数,满分100分)分成四类,并制作了如下的统计图表:
类别 | 甲 | 乙 | 丙 | 丁 |
成绩 | 60≤m<70 | 70≤m<80 | 80≤m<90 | 90≤m<100 |
频数 | 5 | 10 | a | b |
根据图表信息,回答下列问题:
(1)该班共有学生 人,表中a= ,b= ;
(2)扇形图中,丁类所对应的圆心角是 度;
(3)已知A同学在丁类中,现从丁类同学中随机抽两名同学参加学校的决赛,请用列举的方法求A同学能够参加决赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
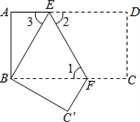
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)若∠1=60°,求∠3的度数;
(2)求证:BE=BF
(3)若AB=6,AD=12,求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程4kx2﹣4kx+k+2=0的两个实数根.是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,请您说明理由.
成立?若存在,求出k的值;若不存在,请您说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1号探测气球从海拔5 m处出发,以l m/min的速度上升.与此同时,2号探测气球从海拔15 m处出发,以0.5 m/min的速度上升,两个气球都匀速上升了50 min.设气球上升的时间为x(min)(0≤x≤50).
(1)根据题意,填写下表:
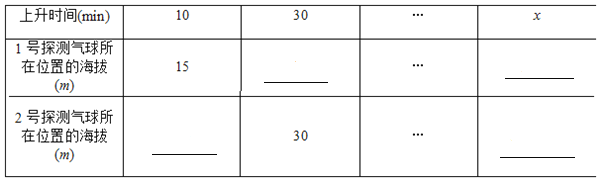
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(3)当30≤x≤50时,两个气球所在位置的海拔最多相差多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com