
【题目】在平面直角坐标系中,一次函数y![]() x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
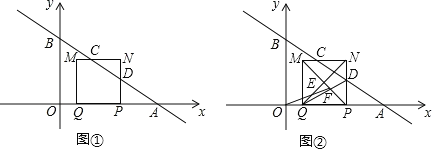
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y![]() x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;
(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
【答案】(1)2;(2)证明见解析;(3)![]() .
.
【解析】
(1)解方程得到OA=6,由t=2,于是得到结论;
(2)根据AP=PQ=t,得到OQ=6-2t,根据正方形的性质得到PQ=QM=MN=PN=t,求得M(6-2t,t),N(6-t,t),C(6-![]() t,t),求得CM=(6-
t,t),求得CM=(6-![]() t)-(6-2t)=
t)-(6-2t)=![]() t,CN=(6-t)-(6-
t,CN=(6-t)-(6-![]() t)=
t)=![]() t,于是得到结论;
t,于是得到结论;
(3)作矩形NEFK,则EN=FK,推出当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,作OH⊥QN于H,解直角三角形即可得到结论.
(1)在y![]() x+4中,令y=0,得x=6,∴OA=6.
x+4中,令y=0,得x=6,∴OA=6.
∵t=2,∴AP=PQ=2,
∴OQ=6﹣2﹣2=2.
故答案为:2;
(2)∵AP=PQ=t,∴OQ=6﹣2t.
∵四边形PQMN是正方形,
∴PQ=QM=MN=PN=t,
∴M(6﹣2t,t),N(6﹣t,t),C(6![]() t,t),
t,t),
∴CM=(6![]() t)﹣(6﹣2t)
t)﹣(6﹣2t)![]() t,
t,
CN=(6﹣t)﹣(6![]() t)
t)![]() t,
t,
∴CM=CN;
(3)作矩形NEFK,则EN=FK.
∵OF+EN=OF+FK,
∴当O,F,K三点共线时,OF+EN=OF+FK的值最小,如图,
作OH⊥QN于H,
在等腰直角三角形PQN中,∵PQ=t,∴QN![]() t,
t,
∴HN=QN﹣QH![]() t﹣(
t﹣(![]() t﹣3
t﹣3![]() )=3
)=3![]() ,
,
∴OF+EN的最小值为:HE+EN=HN=3![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB,△OAB的面积是2.
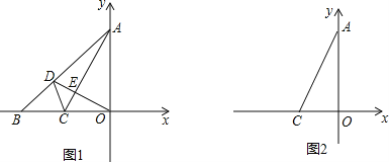
(1)求线段OB的中点C的坐标.
(2)连结AC,过点O作OE⊥AC于E,交AB于点D.
①直接写出点E的坐标.
②连结CD,求证:∠ECO=∠DCB;
(3)点P为x轴上一动点,点Q为平面内一点,以点A.C.P.Q为顶点作菱形,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 | 黄瓜 | 茄子 |
批发价/(元/kg) | 2.4 | 2 |
零售价/(元/kg) | 3.6 | 2.8 |
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
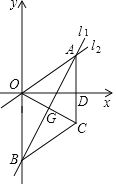
【题目】如图,在平面直角坐标系中,直线l:y![]() x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
(1)求直线l的解析式;
(2)将△OAB沿直线l翻折得到△CAB(其中点O的对应点为点C),求证:AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,0)、(2,0),且﹣2<x1<﹣1,与y轴正半轴的交点在(0,2)的下方,则下列结论:
①abc<0;②b2>4ac;③2a+b+1<0;④2a+c>0.
则其中正确结论的序号是
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示.下列结论:①abc>0;②2a﹣b<0;③4a﹣2b+c<0;④(a+c)2<b2其中正确的个数有( )
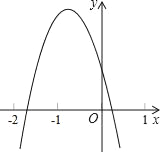
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
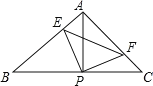
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交边AB,AC于点E,F,当∠EPF在△ABC所在平面内绕顶点P转动时(点E不与A,B重合),给出以下四个结论:①△PFA≌△PEB②EF=AP③△PEF是等腰直角三角形④S四边形AEPF![]() S△ABC,上述结论中始终正确有______.
S△ABC,上述结论中始终正确有______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com