
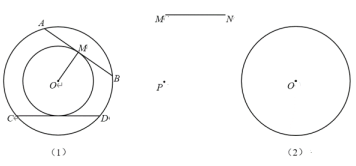
【题目】(1)如图,已知AB、CD是大圆⊙O的弦,AB=CD,M是AB的中点.连接OM,以O为圆心,OM为半径作小圆⊙O.判断CD与小圆⊙O的位置关系,并说明理由;
(2)已知⊙O,线段MN,P是⊙O外一点.求作射线PQ,使PQ被⊙O截得的弦长等于MN.
(不写作法,但保留作图痕迹)
【答案】(1)相切,证明见解析;(2)答案见解析
【解析】
(1)过点O作ON⊥CD,连接OA,OC,根据垂径定理及其推论可得∠AMO=∠ONC=90°,AM=CN,从而求证△AOM≌△CON,从而判定CD与小圆O的位置关系;(2)在圆O上任取一点A,以A为圆心,MN为半径画弧,交圆O于点B,过点O做AB的垂线,交AB于点C,然后以点O为圆心,OC为半径画圆,连接PO,取PO的中点D,以点D为圆心,OD为半径画圆,交以OC为半径的圆于点E,连接PE,交以OA为半径的圆于F,H两点,FH即为所求.
解:(1)过点O作ON⊥CD,连接OA,OC
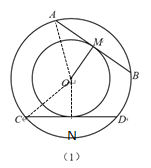
∵AB、CD是大圆⊙O的弦,AB=CD,M是AB的中点,ON⊥CD
∴∠AMO=∠ONC=90°,AM=![]() ,CN
,CN![]() ,
,
∴AM=CN
又∵OA=OC
∴△AOM≌△CON
∴ON=OM
∴CD与小圆O相切
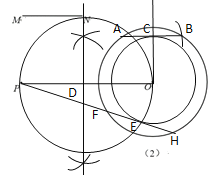
(2)如图FH即为所求


科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出的问题:只有一张电影票,小丽和小芳想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小丽和小芳都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小丽先抽一张,小芳从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小丽看电影,否则小芳看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲同学的方案修改为只用2、3、5、7四张牌,抽取方式及规则不变,乙的方案公平吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
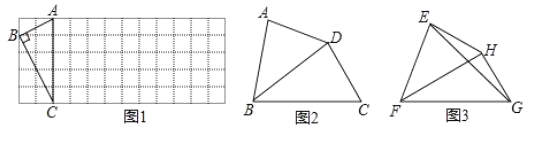
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点 D,使四边形ABCD是以AC为“相似对角线”的四边形(画出1个即可);
(2)如图2,在四边形ABCD中,![]() ,对角线BD平分∠ABC.
,对角线BD平分∠ABC.
求证: BD是四边形ABCD的“相似对角线”;
运用:
(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=![]() .连接EG,若△EFG的面积为
.连接EG,若△EFG的面积为![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中建校80周年,在体育、艺术、科技等方面各具特色,其中排球选修课是体育特色项目之一.体育组老师为了了解初一年级学生的训练情况,随机抽取了初一年级部分学生进行1分钟垫球测试,并将这些学生的测试成绩(即1分钟的垫球个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级(不包括90),90~120范围内的记为C级(不包括120),120~150范围内的记为B级(不包括150),150~180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题:
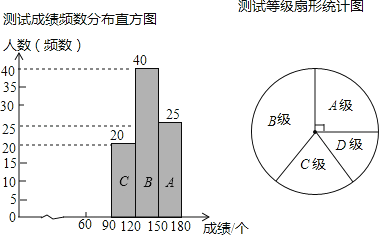
(1)在这次测试中,一共抽取了 名学生,并补全频数分布直方图:在扇形统计图中,D级对应的圆心角的度数为 度.
(2)王攀同学在这次测试中1分钟垫球140个.他为了了解自己垫球个数在年级排名的大致情况,他把成绩为B等的全部同学1分钟垫球人数做了统计,其统计结果如表:
成绩(个) | 120 | 125 | 130 | 135 | 140 | 145 |
人数(频数) | 2 | 8 | 3 | 10 | 9 | 8 |
(垫球个数计数原则:120<垫球个数≤125记为125,125<垫球个数≤130记为130,依此类推)请你估计王攀同学的1分钟垫球个数在年级排名的大致情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
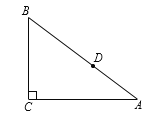
【题目】如图,Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AB边上一点(不与A、B重合),若过点D的直线截得的三角形与△ABC相似,并且平分△ABC的周长,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.

(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
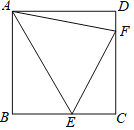
【题目】如图,已知正方形ABCD的边长为5,点E、F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )
A.6+2![]() B.8.5C.10D.12
B.8.5C.10D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com