
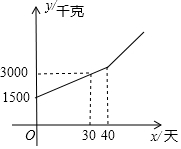
 某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.
某块试验田里的农作物每天的需水量y(千克)与生长时间x(天)之间的关系如折线图所示.这些农作物在刚种植和第30天的需水量分别为1500千克和3000千克,在第40天后每天的需水量比前一天增加100千克.分析 (1)设y=kx+b.把已知坐标代入求出k,b的值.求出y与x的函数关系式;
再根据x的取值求出各段的函数解析式;
(2)令y=4000时,转化为方程求解.
解答 解:(1)当x≤40时,设y=kx+b.
根据题意,得$\left\{\begin{array}{l}{30k+b=3000}\\{b=1500}\end{array}\right.$解这个方程组,得$\left\{\begin{array}{l}{k=50}\\{b=1500}\end{array}\right.$,
∴当x≤40时,y与x之间的关系式是y=50x+1500;
∴当x=40时,y=50×40+1500=3500;
当x>40时,根据题意,得y=100(x-40)+3500,
即y=100x-500.
∴当x>40时,y与x之间的关系式是y=100x-500.
(2)当y=4000时,y与x之间的关系式是y=100x-500.
解不等式100x-500=4000.
得x=45.
∴第45天开始这些农作物的需水量达到4000千克.
点评 本题通过一次函数的知识,考查学生解决实际问题的能力,要求学生根据问题提供的信息读懂图象,并善于从图象中得到正确的信息.要求学生将所给的函数图象与其表示的实际意义联系起来,并结合图象分析和解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
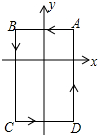 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )| A. | (1,-1) | B. | (-1,1) | C. | (-1,-1) | D. | (0,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
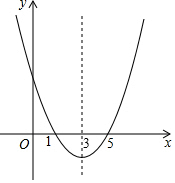 二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3.
二次函数y=ax2+bx+c的图象如图,对称轴为直线x=3,且当x1=$\sqrt{2}$时函数值为y1;x2=π时函数值为y2;当x3=0时函数值为y3;则y1、y2、y3的大小关系是y2<y1<y3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
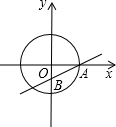 如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).
如图,在平面直角坐标系中,⊙O的直径2$\sqrt{3}$,直线AB的函数解析式为y=$\frac{\sqrt{3}}{3}$x-1,交坐标轴于点A和点B,将线段AB作平移变换,使所得的线段的两端都落在⊙O上,则平移后A点所对应的点的坐标($\frac{\sqrt{2}+\sqrt{3}}{2}$,$\frac{1-\sqrt{6}}{2}$)或($\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{1+\sqrt{6}}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com