
一条直线y=kx+b,其中k+b=-5,kb=6,那么该直线经过( )
A. 第二、四象限 B. 第一、二、三象
C. 第一、三象限 D. 第二、三、四象限
D 【解析】∵k+b=?5、kb=6,∴k<0,b<0∴直线y=kx+b经过二、三、四象限,故选D. 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型:单选题
已知P =2x 2 +4y+13,Q=x 2 -y 2 +6x-1 , 则代数式P,Q的大小关系是( )
A. P≥Q B. P≤Q C. P>Q D. P<Q
C 【解析】P-Q=(2x²+4y+13)-(x²-y²+6x-1) =x²-6x+y²+4y+14 =x²-6x+9+y²+4y+4+1 =(x-3) ²+(y+2)²+1 ∵(x-3)²≥0,(y+2)²≥0, ∴P-Q=(x-3) ²+(y+2)²+1≥1, ∴P>Q.故选C.查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度九年级第一学期期末检测数学试卷 题型:填空题
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为_____mm.

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:解答题
已知一次函数y=kx+b的图象经过点A(-4,0),B(2,6)两点.

(1)求一次函数y=kx+b的表达式;
(2)在直角坐标系中,画出这个函数的图象;
(3)求这个一次函数与坐标轴围成的三角形面积.
(1); (2)函数图像如图: (3)8 【解析】 试题分析:(1)由图象经过两点A(-4,0)、B(2,6)根据待定系数法即得结果; (2)根据两点法即可确定函数的图象; (3)求出图象与x轴及y轴的交点坐标,然后根据直角三角形的面积公式求解即可. (1)∵一次函数y=kx+b的图象经过两点A(-4,0)、B(2,6) ,解得, ∴函数解析式...查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:填空题
函数y=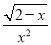 的自变量x的取值范围是__________
的自变量x的取值范围是__________
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:单选题
一次函数y=-3x-2的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
A 【解析】试题分析:根据一次函数的性质,当k>0时,图象经过第一、三象限解答. ∵k=2>0, ∴函数经过第一、三象限, ∵b=﹣3<0,∴函数与y轴负半轴相交, ∴图象不经过第二象限. 故选:B查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
如图,在△ABC中,AD是BC边上的高,tanB=cos∠DAC.
(1)求证:AC=BD;
(2)若sin C= ,BC=12,求△ABC的面积.
,BC=12,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
 的值等于( )
的值等于( )
(A)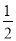 (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第1章 丰富的图形世界 单元测试卷 题型:单选题
(芦溪县期末)如图所示,用一个平面去截一个圆柱,则截得的形状应为( )

A. 
B. 
C. 
D. 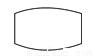
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com