
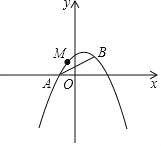
����Ŀ����ͼ����֪������y��ax2+bx+1����A����1��0����B��1��1�����㣮
��1����������ߵĽ���ʽ��
��2���Ķ����⣺
��ͬһƽ��ֱ������ϵ�У�ֱ��l1��y��k1x+b1��k1��b1Ϊ��������k1��0����ֱ��l2��y��k2x+b2��k2��b2Ϊ��������k2��0������l1��l2����k1k2����1��
������⣺
����ֱ��y��2x��1��ֱ��y��mx+2���ഹֱ����m��ֵ��____��
�����������Ƿ���ڵ�P��ʹ�á�PAB����ABΪֱ�DZߵ�ֱ�������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��3��M����������һ���㣬����ֱ��AB���Ϸ�������A��B�غϣ������M��ֱ��AB�ľ�������ֵ��
���𰸡���1��y����![]() x2+
x2+![]() x+1����2����-
x+1����2����-![]() ���ڵ�P�����꣨6����14����4����5������3��
���ڵ�P�����꣨6����14����4����5������3��![]() .
.
��������
��1�����ݴ���ϵ�������ɵú�������ʽ��
��2�����ݴ���Ĺ�ϵ���ɵ�PA��PB�Ľ���ʽ�����ݽⷽ���飬�ɵ�P�����ꣻ
��3�����ݴ�ֱ��x��ֱ���������ľ����ǽϴ�����������С�������꣬�ɵ�MQ�����������ε�������ɵö��κ��������ݶ��κ��������ʣ��ɵ���������ֵ�����������εĵ�һ��ʱ�����߳����ȣ��ɵ������θߵ����ֵ
�⣺��1����A��B��������룬��
![]() ��
��
���![]() ��
��
�����ߵĽ���ʽΪy����![]() x2+
x2+![]() x+1��
x+1��
��2������ֱ��y��2x��1��ֱ��y��mx+2���ഹֱ����
2m����1��
��m����![]() ��
��
�ʴ�Ϊ����![]() ��
��
��AB�Ľ���ʽΪy��![]() x+
x+![]() ��
��
��PA��ABʱ��PA�Ľ���ʽΪy����2x��2��
����PA�������ߣ���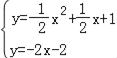 ��
��
���![]() ���ᣩ��
���ᣩ��![]() ��
��
��P��6����14����
��PB��ABʱ��PB�Ľ���ʽΪy����2x+3��
����PB�������ߣ���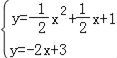 ��
��
���![]() ���ᣩ
���ᣩ![]() ��
��
��P��4����5����
������������PAB����ABΪֱ�DZߵ�ֱ�������Σ���P�����꣨6����14����4����5����
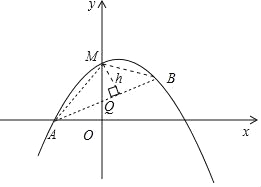
��3����ͼ��
 ��
��
��M��t����![]() t2+
t2+![]() t+1����Q��t��
t+1����Q��t��![]() t+
t+![]() ����
����
��MQ����![]() t2+
t2+![]()
S��MAB��![]() MQ|xB��xA|
MQ|xB��xA|
��![]() ����
����![]() t2+
t2+![]() ����2
����2
����![]() t2+
t2+![]() ��
��
��t��0ʱ��Sȡ���ֵ![]() ����M��0��1����
����M��0��1����
�ɹ��ɶ�������
AB��![]() ��
��![]() ��
��
��M��AB�ľ���Ϊh���������ε��������
h��![]() ��
��![]() ��
��
��M��ֱ��AB�ľ�������ֵ��![]() ��
��


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƽ�С�����ò���Χ��һ�����Ϊ60��2�ľ��οƼ�ABCD������һ��AB��ǽ��ǽ��Ϊ12������AD�ij�Ϊ������DC�ij�Ϊ������
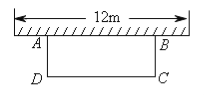
��1��������֮��ĺ�����ϵʽ��
��2����Χ�ɾ��οƼ�ABCD�����߲����ܳ�������26��������AD��DC�ij������������������������������Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
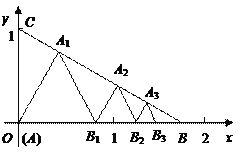
����Ŀ����ͼ��ʾ����֪����A(0��0)��B��![]() ��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������
��0����C��0��1������ABC���������ȱ������Σ�ʹһ����x���ϣ���һ��������BC���ϣ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3���������![]() ���ȱ������εı߳�����__________��
���ȱ������εı߳�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱߡ�ABC��AB=4����ABΪֱ���İ�Բ��BC�߽��ڵ�D������D��DE��AC������ΪE������E��EF��AB������ΪF������FD��
��1����֤��DE�ǡ�O�����ߣ�
��2����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶������ȤС��20λͬѧ��ʵ������еĵ÷������
�÷֣��֣� | 10 | 9 | 8 | 7 |
�������ˣ� | 5 | 8 | 4 | 3 |
��1������20λͬѧʵ������÷ֵ���������λ����
��2����20λͬѧʵ������÷ֵ�ƽ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=8��BC=4�����Խ���BD���е�O��ֱ�߷ֱ�AB��CD�ڵ�E��F������DE��BF��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2�����ı���BEDF������ʱ����EF�ij���
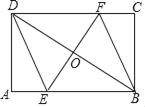
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������Ҫ����������⣮
�ٷ���![]() �Ľ�Ϊ________________��
�Ľ�Ϊ________________��
�ڷ���![]() �Ľ�Ϊ________________��
�Ľ�Ϊ________________��
�۷���![]() �Ľ�Ϊ________________��
�Ľ�Ϊ________________��
��2���������Ϸ�����������������������룺
�ٷ���![]() �Ľ�Ϊ________________��
�Ľ�Ϊ________________��
�ڹ���![]() �ķ���________________�Ľ�Ϊ
�ķ���________________�Ľ�Ϊ![]() ��
��![]() ��
��
��3�������䷽���ⷽ��![]() ������֤������۵���ȷ�ԣ�
������֤������۵���ȷ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���������֤����������
��֪����ͼ��ֱ��AB��CD��ֱ��EF���أ�AB��CD��EGƽ�֡�BEF��FGƽ�֡�DFE��EG��FG���ڵ�G����֤��EG��FG��

֤������AB��CD����֪��
���BEF+��DFE=180�㣨______����
��EGƽ�֡�BEF��FGƽ�֡�DFE����֪����
��______��______��______����
���GEF+��GFE=![]() ����BEF+��DFE����______����
����BEF+��DFE����______����
���GEF+��GFE=![]() ��180��=90�㣨______����
��180��=90�㣨______����
�ڡ�EGF�У���GEF+��GFE+��G=180�㣨______����
���G=180��-90��=90�㣨��ʽ���ʣ���
��EG��FG��______����
��2��������������д����1����֤���⣺______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��y=��2x+3��x�ύ�ڵ�A����ֱ��y=x���ڵ�B��
��1����A������ ������AOB=�� ����
��2����S��OAB��ֵ��
��3������E��ԭ��O��������ÿ��1����λ���ȵ��ٶ�����O��A��·�����յ�A�����˶�������E��EF��x�ύֱ��y=x�ڵ�F������EFΪ��������������EFGH�����˶�t��ʱ��������EFGH����OAB�ص����ֵ����ΪS����S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
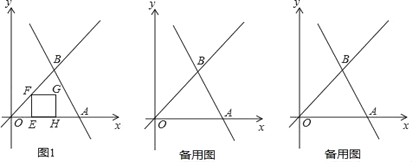
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com