
分析 (1)设面包车购买x辆,根据某汽车租赁公司要购买轿车和面包车共10辆.其中轿车至少要购买5辆,公司可投入的购车款不超过61万元可列不等式求解.
(2)根据求出的方案,可依次求出每种方案的租金,求出符合要求的方案.
解答 解:(1)设轿车要购买x辆,那么面包车要购买(10-x)辆.
由题意得7x+4(10-x)≤61,
解得x≤7.
又∵x≥5,
∴x=5,6,7,
∴购买方案有三种:
方案一:购买轿车5辆,面包车5辆;
方案二:购买轿车6辆,面包车4辆;
方案三:购买轿车7辆,面包车3辆.
(2)方案一的日租金为5×200+5×110=1550(元);
方案二的日租金为6×200+4×110=1640(元);
方案三的日租金为7×200+3×110=1730(元).
因此,为保证日租金不低于1650元,应选择购买方案三.
点评 本题考查一元一次不等式的应用和理解题意的能力,关键轿车和面包车的数量关系做为不等量关系,以及购车款做为不等量关系列不等式求解,求出每种方案租金收入,从而可求出购买方案.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
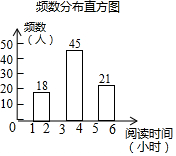 在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:| 阅读时间 (小时) | 频数 (人) | 频率 |
| 1≤x<2 | 18 | 0.12 |
| 2≤x<3 | a | m |
| 3≤x<4 | 45 | 0.3 |
| 4≤x<5 | 36 | n |
| 5≤x<6 | 21 | 0.14 |
| 合计 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com