
【题目】在平面直角坐标系xOy中,直线x=3与直线y=![]() x+1交于点A,函数y=
x+1交于点A,函数y=![]() (k>0,x>0)的图象与直线x=3,直线y=
(k>0,x>0)的图象与直线x=3,直线y=![]() x+1分别交于点B,C.
x+1分别交于点B,C.
(1)求点A的坐标.
(2)横、纵坐标都是整数的点叫做整点.记函数y=![]() (k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
(k>0,x>0)的图象在点B,C之间的部分与线段AB,AC围成的区域(不含边界)为W.
①当k=1时,结合函数图象,求区域W内整点的个数;
②若区域W内恰有1个整点,直接写出k的取值范围.
【答案】(1)A(3,![]() );(2)①在W区域内有1个整数点;②当区域W内恰有1个整点时,1≤k<2或16<k≤20
);(2)①在W区域内有1个整数点;②当区域W内恰有1个整点时,1≤k<2或16<k≤20
【解析】
(1)根据题意列方程即可得到结论;
(2)①当k=1时,求得B、C的坐标,根据图象得到结论;
②分两种情况根据图象即可得到结论.
解:(1)直线x=3与直线y=![]() x+1交于点A,
x+1交于点A,
∴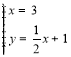 ,解得
,解得![]() ,
,
∴A(3,![]() );
);
(2)①当k=1时,根据题意B(3,![]() ),C(
),C(![]() ,
,![]() ),
),
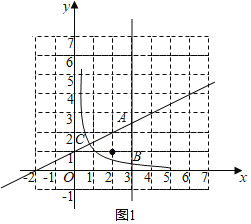
由图像可得,在W区域内有1个整数点:(2,1);
②若区域W内恰有1个整点,
当C点在直线x=3的左边时,如图1,在W区域内有1个整数点:(2,1),
∴1≤k<2;
当C点在直线x=3的右边时,如图2,在W区域内有1个整数点:(4,4),
∴16<k≤20;
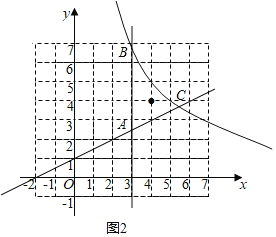
综上,当区域W内恰有1个整点时,1≤k<2或16<k≤20


科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 在射线
在射线![]() 上,点
上,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合).点
重合).点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() 和
和![]() ,点
,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .小明在探究图形运动的过程中发现:
.小明在探究图形运动的过程中发现:![]() 始终成立.
始终成立.

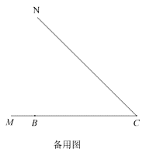
(1)如图1,当![]() 时;
时;
①求证:![]() ;
;
②用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)当![]() 时,直接用等式表示线段
时,直接用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系是______.
之间的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F.
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明;
(3)连接CE,若AB=2![]() ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宜跟几位同学在某快餐厅吃饭,如图为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.
(1)他们点了 份A套餐, 份B套餐, 份C套餐(均用含x或y的代数式表示);
(2)若x=6,且A、B、C套餐均至少点了1份,则最多有 种点餐方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离.
(1)已知点A(1,2)、B(0,﹣5)、C(2,﹣1)、D(3,4).
①与直线y=3x﹣5相离的点是 ;
②若直线y=3x+b与△ABC相离,求b的取值范围;
(2)设直线y=![]() x+3、直线y=﹣
x+3、直线y=﹣![]() x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
x+3及直线y=﹣2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.
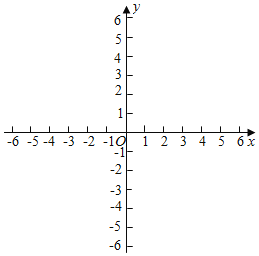
查看答案和解析>>
科目:初中数学 来源: 题型:
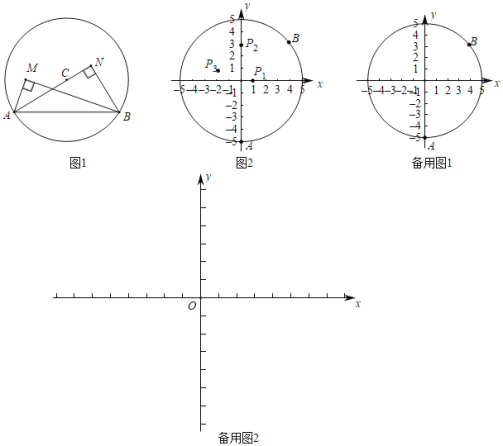
【题目】A,B是⊙C上的两个点,点P在⊙C的内部.若∠APB为直角,则称∠APB为AB关于⊙C的内直角,特别地,当圆心C在∠APB边(含顶点)上时,称∠APB为AB关于⊙C的最佳内直角.如图1,∠AMB是AB关于⊙C的内直角,∠ANB是AB关于⊙C的最佳内直角.在平面直角坐标系xOy中.
(1)如图2,⊙O的半径为5,A(0,﹣5),B(4,3)是⊙O上两点.
①已知P1(1,0),P2(0,3),P3(﹣2,1),在∠AP1B,∠AP2B,∠AP3B,中,是AB关于⊙O的内直角的是 ;
②若在直线y=2x+b上存在一点P,使得∠APB是AB关于⊙O的内直角,求b的取值范围.
(2)点E是以T(t,0)为圆心,4为半径的圆上一个动点,⊙T与x轴交于点D(点D在点T的右边).现有点M(1,0),N(0,n),对于线段MN上每一点H,都存在点T,使∠DHE是DE关于⊙T的最佳内直角,请直接写出n的最大值,以及n取得最大值时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图都改变
查看答案和解析>>
科目:初中数学 来源: 题型:
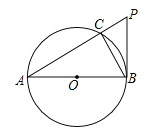
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数y=x+4的图象与y轴交于点A,与反比例函数y=![]() 的图象的一个交点为M.
的图象的一个交点为M.
(1)求点A的坐标;
(2)连接OM,如果△MOA的面积等于2,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com