
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 . 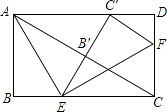
【答案】![]()
【解析】解:连接CC′, ∵将△ABE沿AE折叠,使点B落在AC上的点B′处,
又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.
∴EC=EC′,
∴∠1=∠2,
∵∠3=∠2,
∴∠1=∠3,
∵∠CB′C′=∠D=90°,
∴△CC′B′≌△CC′D,
∴CB′=CD,
又∵AB′=AB,
∴AB′=CB′,
所以B′是对角线AC中点,
即AC=2AB,
所以∠ACB=30°,
∴∠BAC=60°,
∴tan∠BAC=tan60°= ![]() =
= ![]() ,
,
BC:AB的值为: ![]() .
.
故答案为: ![]() .
.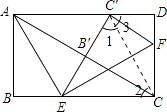
首先连接CC′,可以得到CC′是∠EC′D的平分线,所以CB′=CD,又AB′=AB,所以B′是对角线中点,AC=2AB,所以∠ACB=30°,即可得出答案.


科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,直线c与a、b都相交,从所标识的∠1、∠2、∠3、∠4、∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:∠1=∠2,∠3+∠4= 180°;确定直线a,c的位置关系,并说明理由;
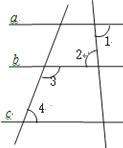
解:a c;
理由:∵∠1=∠2( ),
∴ a // ( );
∵ ∠3+∠4= 180°( ),
∴ c // ( );
∵ a // ,c // ,
∴ // ( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系内,画在透明胶片上的ABCD,点A的坐标是(0,2).现将这张胶片平移,使点A落在点A′(5,﹣1)处,则此平移可以是( )
A.先向右平移5个单位,再向下平移1个单位
B.先向右平移5个单位,再向下平移3个单位
C.先向右平移4个单位,再向下平移1个单位
D.先向右平移4个单位,再向下平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.
(1)求证:△AFG∽△AED
(2)若FG=2,G为AD中点,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
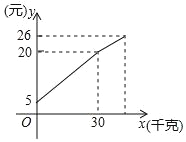
【题目】王大爷带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价出售一些后,又降价出售,售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示.根据图象回答下列问题:
(1)王大爷自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(4)写出售出土豆的千克数x与他手中持有的钱数y(含备用零钱)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面四个整式中,不能表示图中阴影部分面积的是( )

A. (x+3)(x+2)﹣2x B. x(x+3)+6 C. 3(x+2)+x2 D. x2+5x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆车长为4米的小轿车和一辆车长为20米的大货车,在长为1200米隧道的两个入口同时开始相向而行,小轿车的速度是大货车速度的3倍,大货车速度为10米/秒.
(1)求两车相遇的时间;
(2)求两车从相遇到完全离开所需的时间;
(3)当小轿车车头和大货车车头相遇后,求小轿车车头与大货车车头的距离是小轿车车尾与大货车车尾的距离的4倍时所需的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com