
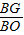 =
= ,
,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
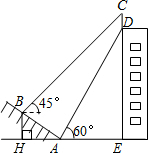 (2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
(2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:| 3 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
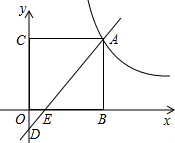 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
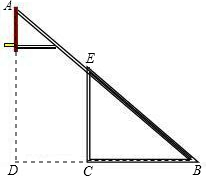
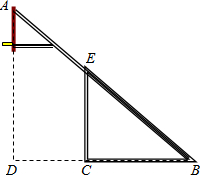 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com