【题目】如图，已知
，
，若
平分
，
平分
，且
，则为___________°．
【答案】
【解析】
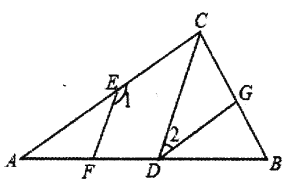
根据平行线的性质即可得出∠1＋∠ACD＝180°，再根据条件∠1＋∠2＝180°，即可得到∠ACD＝∠2，进而判定AC∥DG．根据平行线的性质，得到∠BDG＝∠A＝40°，根据三角形外角性质，即可得到∠ACD＝∠BDC∠A＝40°，再根据角平分线的定义，即可得出∠ACB的度数．
解：∵EF∥CD
∴∠1＋∠ACD＝180°，
又∵∠1＋∠2＝180°，
∴∠ACD＝∠2，
∴AC∥DG．
∴∠BDG＝∠A＝40°，
∵DG平分∠CDB，
∴∠CDB＝2∠BDG＝80°，
∵∠BDC是△ACD的外角，
∴∠ACD＝∠BDC∠A＝80°40°＝40°，
∵CD平分∠ACB，
∴∠ACB＝2∠ACD＝80°．
故答案为：80．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线l1：y=﹣
x+1与x轴，y轴分别交于点A和点B，直线l2：y=kx（k≠0）与直线l1在第一象限交于点C．若∠BOC=∠BCO，则k的值为（ ）
A. 
B. 
C. 
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】说理填空：如图，点E是DC的中点，EC=EB，∠CDA=120°，DF//BE，且DF平分∠CDA，若△BCE的周长为18cm，求DC的长．
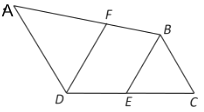
解： 因为DF平分∠CDA,（已知）
所以∠FDC=
∠_________.（____________________）
因为∠CDA=120°,（已知）所以∠FDC=______°.
因为DF//BE,（已知）
所以∠FDC=∠_________=60°.（____________________________________）
又因为EC=EB,（已知）
所以△BCE为等边三角形.（________________________________________）
因为△BCE的周长为18cm,（已知） 所以BE=EC=BC=6 cm.
因为点E是DC的中点,（已知） 所以DC=2EC=12 cm .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示， 
是
的角平分线，以点
为圆心， 
为半径作圆交
的延长线于点
，交
于点
，交
于点
，且
．
（
）求证： 
；
（
）求证：点
是
的中点；
（
）如果
，求半径
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从我市至枣庄正在修筑的高速公路经过某村，需把本村部分农户搬迁至一个规划区域建房．若这批搬迁农户建房每户占地
，则规划区域内绿地面积占规划区域总面积的
；政府又鼓励本村不需要搬迁的农户到规划区域建房，这样又有
户农户加入建房，若仍以每户占地计算，则这时绿地面积只占规划区域总面积的
．问：
（1）（列方程组解应用题）最初必须搬迁建房的农户有多少，政府的规划区域总面积是多少平方米？
（2）若要求绿地面积不得少于规划区域总面积的
，为了符合要求，需要退出部分农户，至少需要退出几户农户？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
