
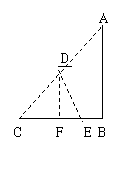
如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮.两船同时起航,并同时到达折线A-B-C上的某点E处.已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
(A)在线段AB上;(B)在线段BC上;(C)可以在线段AB上,也可以在线段BC上;
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)
解:(1)由于客轮的速度是货轮的2倍,所以客轮行驶的距离是货轮行驶距离的2倍,如果相遇点E在AB上,则D到E的距离大于或等于100海里,AE小于或等于200,当货轮行驶 100海里到AB中点时,客轮已行驶200海里到达点B,两船不可能相遇.故可知相遇点E在BC上,应选B;
(2)设货轮从出发到两船相遇共航行了x海里,过D作DF⊥BC于F,连结DE,则DE=x,AB+BE=2x,BE=2x-200;
在等腰直角三角形ABC中,因为AB=BC=200,D是AB的中点,
所以,DF=100,EF=BF-BE=100-(2x-200)=300-2x,
在直角三角形DEF中,由勾股定理,得
![]() ,解之,得x=200±
,解之,得x=200±![]() ,
,
因为200+![]() >200,所以,x=200-
>200,所以,x=200-![]() .
.
答:货轮从出发到两船相遇共航行了(200-![]() )海里.
)海里.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com