16.
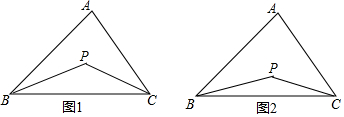
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【分析问题】在解决这个问题时,某小组同学是这样做的:
先赋予∠A几个特殊值:
当∠A=80°时,计算出∠P=130°;
当∠A=40°时,计算出∠P=110°;
当∠A=100°时,计算出∠P=140°;
…由以上特例猜想∠P与∠A的关系为:∠P=90°+$\frac{1}{2}$∠A.再证明这一结论:
证明:∵点P是∠ABC、∠ACB的角平分线的交点.
∴∠PBC=$\frac{1}{2}$∠ABC;∠PCB=$\frac{1}{2}$∠ACB
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)
又∵∠A+(∠ABC+∠ACB)=180°
∴∠ABC+∠ACB=180°-∠A
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)
=$\frac{1}{2}$(180°-∠A)
∴∠P=180°-(∠PBC+∠PCB)
=180°-$\frac{1}{2}$(180°-∠A)
=90°+$\frac{1}{2}$∠A
【解决问题】请运用以上解决问题的“思想方法”解决下面的几个问题:
(1)如图2,若点P时∠ABC、∠ACB的三等分线的交点,即∠PBC=$\frac{1}{3}$∠ABC,∠PCB=$\frac{1}{3}$∠ACB,猜测∠P与∠A的关系为∠P=$\frac{1}{3}$∠A+$\frac{2}{3}$×180°,证明你的结论.
(2)若点P时∠ABC、∠ACB的四等分线的交点,即∠PBC=$\frac{1}{4}$∠ABC,∠PCB=$\frac{1}{4}$∠ACB,则∠P与∠A的关系为∠P=$\frac{1}{4}$∠A+$\frac{3}{4}$×180°.(直接写出答案,不需要证明)
(3)若点P时∠ABC、∠ACB的n等分线的交点,即∠PBC=$\frac{1}{n}$∠ABC,∠PCB=$\frac{1}{n}$∠ACB,则∠P与∠A的关系为$\frac{n-1}{n}$•180°+$\frac{1}{n}$∠A.(直接写出答案,不需要证明)

 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
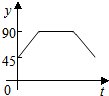
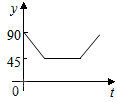
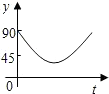
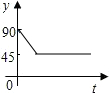
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗? 如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )
如图,点A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿线段OC-弧CD-线段DO的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度,则下列图象中表示y与t的函数关系最恰当的是( )