
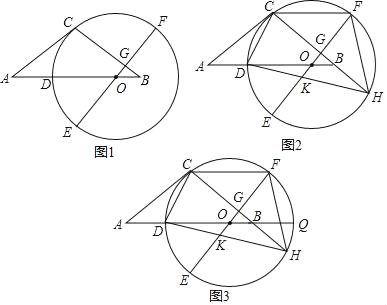
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
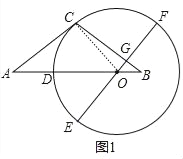
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
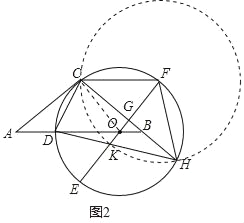
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】(1)如图1中,连接OC,根据等角的余角相等,证明即可.
(2)如图2中,连接OC,首先证明,再证明点K在以F为圆心FC为半径的圆上即可解决问题;
(3)如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF= ![]() ,OG=2-x,GF=
,OG=2-x,GF=![]() ,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
,根据CG2=CF2-FG2=CO2-OG2,列出方程求出x,再想办法求出HM、MQ即可解决问题.
(1)证明:如图1中,连接OC.
∵AC是⊙O的切线,
∴OC⊥AC,
∴∠ACO=90°,
∴∠A+∠AOC=90°,
∵CA=CB,
∴∠A=∠B,
∵EF⊥BC,
∴∠OGB=90°,
∴∠B+∠BOG=90°,
∴∠BOG=∠AOC,
∵∠BOG=∠DOE,
∴∠DOC=∠DOE,
∴点D是![]() 的中点.
的中点.
(2)证明:如图2中,连接OC.
∵EF⊥HC,
∴CG=GH,
∴EF垂直平分HC,
∴FC=FH,
∵∠CFK=![]() ∠COE,
∠COE,
∵∠COD=∠DOE,
∴∠CFK=∠COD,
∵∠CHK=![]() ∠COD,
∠COD,
∴∠CHK=![]() ∠CFK,
∠CFK,
∴点K在以F为圆心FC为半径的圆上,
∴FC=FK=FH,
∵DO=OF,
∴DO+OK=OF+OK=FK=CF,
即CF=OK+DO;
(3)解:如图3中,连接OC、作HM⊥AQ于M.设OK=x,则CF=![]() +x,OG=2﹣x,GF=
+x,OG=2﹣x,GF=![]() ﹣(2﹣x),
﹣(2﹣x),

∵CG2=CF2﹣FG2=CO2﹣OG2,
∴(![]() +x)2﹣[
+x)2﹣[![]() (2﹣x)]2=(
(2﹣x)]2=(![]() )2﹣(2﹣x)2,
)2﹣(2﹣x)2,
解得x=![]() ,
,
∴CF=5,FG=4,CG=3,OG=![]() ,
,
∵∠CFE=∠BOG,
∴CF∥OB,
∴![]() =
=![]() =
=![]() ,
,
可得OB=![]() ,BG=
,BG=![]() ,BH=
,BH=![]() ,
,
由△BHM∽△BOG,可得![]() =
=![]() =
=![]() ,
,
∴BM=![]() ,HM=
,HM=![]() ,MQ=OQ﹣OB﹣BM=
,MQ=OQ﹣OB﹣BM=![]() ,
,
在Rt△HMQ中,QH=![]() =
=![]() =
=![]()
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售![]() 元,在果园每千克售
元,在果园每千克售![]() 元
元![]() .该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
.该农户将水果拉到市场出售平均每天出售1000千克,需8人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用![]() 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
元,且两种方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
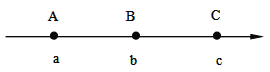
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果![]() ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图乙,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)如图甲,将△ADE绕点A 旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是_____.
①BD=CE②BD⊥CE③∠ACE+∠DBC=45°④BE2=2(AD2+AB2)
(2)若AB=4,AD=2,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②求旋转过程中线段PB长的最大值.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.

(1)根据图象,求y与x之间的函数关系式;
(2)求甲、乙两种品牌的文具盒进货单价;
(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
在“平行四边形、菱形、矩形、正方形”中是“等邻边四边形”的是 .
(2)概念应用
在Rt△ABC中,∠C=![]() ,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .
,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.请根据以上信息解答下列问题:
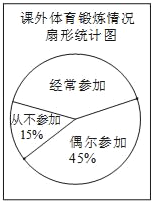

(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为_____;
(2)请补全条形统计图;
(3)该校共有1000名男生,小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1000×![]() =90”,请你判断这种说法是否正确,并说明理由.
=90”,请你判断这种说法是否正确,并说明理由.
(4)若要从被调查的“从不参加”课外体育锻炼的男生中随机选择10名同学组成课外活动小组,则从不参加活动的小王被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
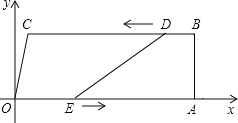
【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com