
分析 半径为16cm,圆心角为90°的扇形的弧长是$\frac{90π×16}{180}$=8π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是8π,设圆锥的底面半径是r,则得到2πr=8π,求出r的值即可.
解答 解:∵$\frac{90π×16}{180}$=8π,
圆锥的底面周长等于侧面展开图的扇形弧长,
∴圆锥的底面周长是8ππcm,
设圆锥的底面半径是r,
则得到2πr=8π,
解得:r=4(cm).
故答案为:4.
点评 本题考查了有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
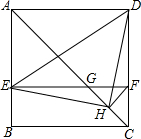 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若$\frac{AE}{AB}$=$\frac{1}{3}$,则3S△EDH=13S△DHC,其中结论正确的有①②③(填写序号).
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若$\frac{AE}{AB}$=$\frac{1}{3}$,则3S△EDH=13S△DHC,其中结论正确的有①②③(填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
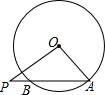 如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$.
如图,已知⊙O的半径为6,弦AB的长为8,P是AB延长线上一点,BP=2,则tan∠OPA的值是$\frac{{\sqrt{5}}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
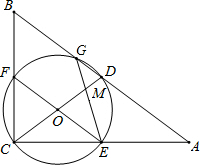 如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G、F、E点,GE,CD的交点为M,且ME=4$\sqrt{6}$,MD:CO=2:5.
如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G、F、E点,GE,CD的交点为M,且ME=4$\sqrt{6}$,MD:CO=2:5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com