
����Ŀ����14�֣���ͼ1����ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������B���߶�AE�ϣ���C���߶�AD�ϣ�
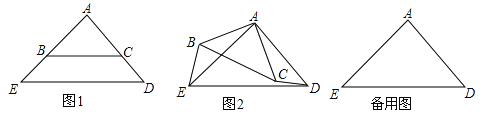
��1����ֱ��д���߶�BE���߶�CD�Ĺ�ϵ�� ��
��2����ͼ2����ͼ1�е���ABC�Ƶ�A˳ʱ����ת������0������360������
����1���еĽ����Ƿ��������������������ͼ2֤����������������˵�����ɣ�
����AC=![]() EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
EDʱ��̽������ABC��ת�Ĺ����У��Ƿ���������Ľ�����ʹ��A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�������Ķ������������ڣ���˵�����ɣ�
���𰸡���1��BE=CD����2���������������ڣ���=45����
��������
���⣨1������ABC����AED���ǵ���ֱ�������Σ��õ�AB=AC��AE=AD�����ɵõ�BE=CD��
��2��������ABC����AED���ǵ���ֱ�������Σ��õ�AB=AC��AE=AD������ת�����ʿɵ���BAE=��CAD���õ���BAE�ա�CAD������ȫ�������ε����ʼ��ɵõ����ۣ�
����ƽ���ı��ε����ʿɵ���ABC=��ADC=45�������ɵ���ֱ�������ε����ʼ��ɵõ����ۣ�
�����������1���ߡ�ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������AB=AC��AE=AD����AE��AB=AD��AC����BE=CD��
��2�����������������£�
�ߡ�ABC����AED���ǵ���ֱ�������Σ���BAC=��EAD=90������AB=AC��AE=AD������ת�����ʿɵ���BAE=��CAD������BAE����CAD�У���AB=AC����BAE=��CAD��AE=AD�����BAE�ա�CAD��SAS������BE=CD��
�����ڣ���=45��������A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı��Σ����ABC=��ADC=45������AC=![]() ED�����CAD=45�����������Ķ�����45����
ED�����CAD=45�����������Ķ�����45����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC������AC=6cm��BC=8cm��AB=10cm����AB���ϵ�����Ϊ_____cm��AB���ϵĸ�Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�ټ����ض�ͯ������ڣ����ϰ��мס����������ӣ�ÿ����ʢ�а���2������ɳ��1��������1�������������ȫһ������
��1��С���Ӽ�������ȡһ�����ӣ�ȡ����ɳ�յĸ����� ��
��2��С���ڼ��̺��������Ⱥ��ȡ��һ�����ӣ�������״ͼ���б�����С��ǡ��ȡ�����������ӵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ��-1,3������-4,1����(-2,1)���Ƚ���ABC��һȷ������ƽ�Ƶõ���A![]() B
B![]() C
C![]() ����B�Ķ�Ӧ��B
����B�Ķ�Ӧ��B![]() ��������(1,2)���ٽ���A
��������(1,2)���ٽ���A![]() B
B![]() C
C![]() ��ԭ��O˳ʱ����ת90��õ���A
��ԭ��O˳ʱ����ת90��õ���A![]() B
B![]() C
C![]() ,��A
,��A![]() �Ķ�Ӧ��Ϊ��A
�Ķ�Ӧ��Ϊ��A![]() .
.
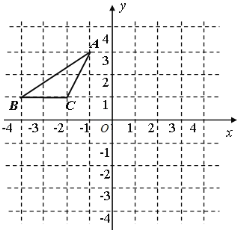
(1) ������A![]() B
B![]() C
C![]() ��
�� ![]()
(2) ������A![]() B
B![]() C
C![]() ��
��
(3) ����������α任�����У���A������A![]() �����A
�����A![]() ��·���ܳ�.
��·���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC����AB=BC����BCΪֱ���ġ�O��AC�ཻ�ڵ�D������D��DE��AB��CB�ӳ����ڵ�E������Ϊ��F.
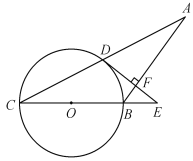
��1���ж�DE���O��λ�ù�ϵ����˵�����ɣ�
��2������O�İ뾶R=5����tanC =![]() ����EF�ij�.
����EF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����A��36�㣬BDƽ�֡�ABC��CEƽ�֡�ACB��CE��BD�ڵ�O����ôͼ�еĵ��������θ�����������
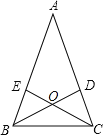
A.4B.6C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱�֤���������������к���ˮ��˳���ٰ죬ij���Ź�����Ա�˿�ͧ������ˮ��ˮ�飬��ÿ��10���ٶ���ƽ���ڰ��ߵ�����AB��������ʻ����A����ð���һ������P�ڱ�ƫ��30�������ϣ�������ʻ40�뵽��B��ʱ����ý�����P�ڱ�ƫ��60�������ϣ���ͼ��ʾ��������P������AB�ľ��루����������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��ֽƬ���۵���ʹ��B��AD���ϵĵ�K�غϣ�EGΪ�ۺۣ���C��AD���ϵĵ�K�غϣ�FHΪ�ۺۣ���֪��1=67.5�㣬��2=75�㣬EF=![]() +1����BC�ij���
+1����BC�ij���
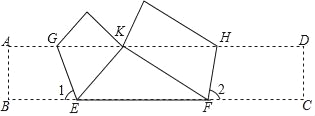
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͬһ����ϵ�£�һ�κ���![]() ����κ���
����κ���![]() ��ͼ����¿����ǣ�������
��ͼ����¿����ǣ�������
A.  B.
B. 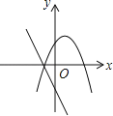 C.
C.  D.
D. 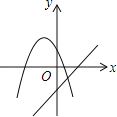
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com