
分析 (1)(2)(3)应用乘法分配律,求出每个算式的值各是多少即可.
(4)首先把每个加数分成两个分数的差的形式,然后应用加法结合律,求出算式的值是多少即可.
解答 解:(1)(-18)×(-$\frac{1}{9}$+$\frac{2}{3}$-$\frac{1}{6}$)
=(-18)×(-$\frac{1}{9}$)+(-18)×$\frac{2}{3}$-(-18)×$\frac{1}{6}$
=2-12+3
=-7
(2)(-61$\frac{17}{18}$)×9
=(-62+$\frac{1}{18}$)×9
=(-62)×9+$\frac{1}{18}$×9
=-558+$\frac{1}{2}$
=-557$\frac{1}{2}$
(3)-2$\frac{1}{6}$×5-2$\frac{1}{6}$×(-4)+$\frac{13}{6}$×(-8)
=$\frac{13}{6}$×(-5+4-8)
=$\frac{13}{6}$×(-9)
=-19$\frac{1}{2}$
(4)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2004×2005}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2004}$-$\frac{1}{2005}$
=1-$\frac{1}{2005}$
=$\frac{2004}{2005}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
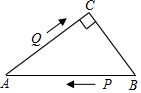 如图,在Rt△ABC中,∠C=90°,AB=10cm,sin∠B=$\frac{4}{5}$.点P从点B出发沿BA方向向点A运动,速度为1cm/s,同时点Q从点A出发沿A→C→B方向向点B运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠C=90°,AB=10cm,sin∠B=$\frac{4}{5}$.点P从点B出发沿BA方向向点A运动,速度为1cm/s,同时点Q从点A出发沿A→C→B方向向点B运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.设点P的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 任意打开九年级上册数学教科书,正好是56页是确定事件 | |
| D. | 一只盒子中有白球m个,红球5个,黑球n个(每个球除了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-5x+4=0 | B. | 3x2-5x+4=0 | C. | x2+2x+4=0 | D. | x2-5x+4=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com