
【题目】(1)用“*”表示一种新运算:对于任意正实数a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
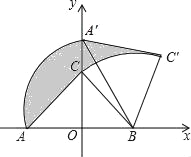
【题目】如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=2,则阴影部分面积为( )
A. ![]() π B.
π B. ![]() π﹣1 C.
π﹣1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
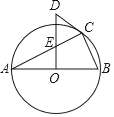
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校九年级举行乒乓球比赛,准备发放一些奖品进行奖励,奖品设为一等奖和二等奖.已知购买一个一等奖奖品比购买一个二等奖奖品多用20元.若用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半.
(1)求购买一个一等奖奖品和一个二等奖奖品各需多少元?
(2)经商谈,商店决定给予该学校购买一个一等奖奖品即赠送一个二等奖奖品的优惠,如果该学校需要二等奖奖品的个数是一等奖奖品个数的2倍还多8个,且该学校购买两个奖项奖品的总费用不超过670元,那么该学校最多可购买多少个一等奖奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
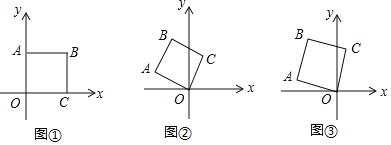
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点.
(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
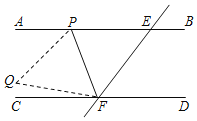
【题目】如图,直线AB∥CD,直线l与直线AB、CD相交于点E、F,P是射线EA上的一个动点(不包括端点E),将△EFP沿PF折叠,便顶点E落在点Q处.若∠PEF=54°,且∠CFQ=![]() ∠CFP,则∠PFE的度数是_____.
∠CFP,则∠PFE的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
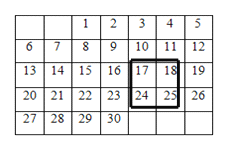
【题目】仔细观察下面的日历,回答下列问题:
(1)任意用正方形框圈出四个日期,如果正方形框中的第一个数(左上角的数)为![]() ,用代数式表示正方形框中的四个数的和;
,用代数式表示正方形框中的四个数的和;
(2)若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于![]() 吗?如果能,依次写出这四个数;如果不能,请说明理由.
吗?如果能,依次写出这四个数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
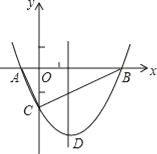
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com