
【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.
(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】(1)m=3;(2)点A的坐标为(1,4),点B的坐标为(6,9); (3)存在,P(![]() ,
, ![]() ).
).
【解析】试题分析:(1)由顶点在x轴上知它与x轴只有一个交点,即对应一元二次方程中△=0,可得关于m的方程,求解即可得m;
(2)联立抛物线与直线解析式可得方程组,求解即可得A、B坐标;
(3)设点P(a,b),作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,分别表示出AR、BS、RC、CS、RS、PT、RT、ST的长,根据S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS求出S△ABC,由S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP表示出S△PAB,根据△PAB的面积是△ABC面积的2倍可得a、b间关系,代入抛物线解析式即可求得.
试题解析:(1)∵抛物线的顶点在x轴上,
∴它与x轴只有一个交点,
∴(m+3)2﹣4×9=0,
解得m=3或m=﹣9,
又∵抛物线对称轴大于0
∴﹣![]() >0,即m>﹣3,
>0,即m>﹣3,
∴m=3;
(2)由(1)可得抛物的解析式为y=x2﹣6x+9,
解方程组![]() ,解得
,解得![]() 或
或![]() ,
,
∴点A的坐标为(1,4),点B的坐标为(6,9);
(3)存在,
设点P(a,b),如图,作PT⊥x轴交BD于点E,AR⊥x轴,BS⊥x轴,
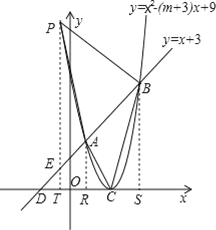
∵A(1,4),B(6,9),C(3,0),P(a,b)
∴AR=4,BS=9,RC=3﹣1=2,CS=6﹣3=3,RS=6﹣1=5,PT=b,RT=1﹣a,ST=6﹣a,
∴S△ABC=S梯形ARSB﹣S△ARC﹣S△BCS=![]() ×(4+9)×5﹣
×(4+9)×5﹣![]() ×2×4﹣
×2×4﹣![]() ×3×9=15,
×3×9=15,
S△PAB=S梯形PBST﹣S梯形ABSR﹣S梯形ARTP
=![]() ×(9+b)(6﹣a)﹣
×(9+b)(6﹣a)﹣![]() ×(4+9)×5﹣
×(4+9)×5﹣![]() ×(b+4)(1﹣a)
×(b+4)(1﹣a)
=![]() (5b﹣5a﹣15),
(5b﹣5a﹣15),
又∵S△PAB=2S△ABC,∴![]() (5b﹣5a﹣15)=30,∴b﹣a=15,b=15+a,
(5b﹣5a﹣15)=30,∴b﹣a=15,b=15+a,
∵点P在抛物线上∴b=a2﹣6a+9,∴15+a=a2﹣6a+9,
∴a2﹣7a﹣6=0,解得:a=![]() ,
,
∵﹣3<a<1,∴a=![]() ,∴b=15+a=
,∴b=15+a=![]() ,
,
∴P(![]() ,
, ![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 3(x-y)=3x-y B. (x+2)(x-2)=x2-2
C. (a+b)2=a2+b2 D. (x-y)2=x2-2xy+y2
查看答案和解析>>
科目:初中数学 来源: 题型:
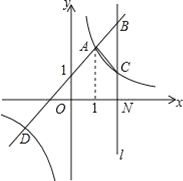
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,点D是⊙O上的一点,点C是![]() 的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
的中点,弦CM垂直AB于点F,连接AD,交CF于点P,连接BC,∠DAB=30°
(1)求∠ABC的度数;
(2)若CM=8![]() ,求
,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com